Recall that isoperimetric functions of a finitely presented group
![]() measure areas of van Kampen diagrams over the presentation of
this group. Figure 1 shows what
a van Kampen diagram may look like.
measure areas of van Kampen diagrams over the presentation of
this group. Figure 1 shows what
a van Kampen diagram may look like.
![\begin{picture}(118.47,59.67)
\put(80.17,29.83){\oval(75.67,51.00)[]}
\put(42.33...
...,35.33){\vector(-1,0){3.33}}
\put(45.00,35.33){\vector(1,0){4.67}}
\end{picture}](img2.gif)
It is a directed planar labeled graph where every edge is labeled by a
generator from X, and the contour of every 2-cell (face) is labeled by a
relator from R. By van Kampen lemma [25] a word
![]() is equal
to 1 in the group G if and only if there exists a van Kampen diagram
is equal
to 1 in the group G if and only if there exists a van Kampen diagram ![]() over the
presentation of G with boundary label w. The number of cells in
over the
presentation of G with boundary label w. The number of cells in ![]() is equal to the number of factors in a representation of w as a
product of conjugates of relators from R:
is equal to the number of factors in a representation of w as a
product of conjugates of relators from R:
If a van Kampen diagram has minimal number of cells, n, among all diagrams
with the same boundary label w then we say that w has area n. A
function f(m) is called an isoperimetric function of
the presentation
![]() of
the group G if every word of length at most m which is equal to 1 in the
group has area at most f(m). On the set of functions
of
the group G if every word of length at most m which is equal to 1 in the
group has area at most f(m). On the set of functions
![]() ,
one can define a quasi-order saying that
,
one can define a quasi-order saying that ![]() if
if
We can also define isodiametric functions introduced by Gersten
[16]. These functions measure the diameter of a van Kampen
diagram with given perimeter2.
More precisely, with every word w which is equal to 1 in G, we associate
its diameter, that is the smallest diameter of a van Kampen diagram with
boundary label w. Then if d(n) is an isodiametric function of
![]() ,
d(n) must exceed the diameter of every word w= 1 (mod
G) of length
,
d(n) must exceed the diameter of every word w= 1 (mod
G) of length ![]() .
The equivalence of isodiametric functions is
defined as before. Isodiametric functions of different finite presentations of the
same group are always equivalent [19].
.
The equivalence of isodiametric functions is
defined as before. Isodiametric functions of different finite presentations of the
same group are always equivalent [19].
Both isoperimetric and isodiametric functions reflect the decidability of
the word problem in the group. In particular it is well known (see, for example, [26]) that the word
problem is decidable if and only if the Dehn function (the smallest
isodiametric function) is recursive. Nevertheless, the word problem in a
group with huge Dehn function may be easy. For example the word problem in
the Baumslag-Solitar group
![]() can be solved
in quadratic time (since this group is representable by
can be solved
in quadratic time (since this group is representable by ![]() integer
matrices) while the Dehn function is exponential [11]. One of our
main goals is to show that still there exists a very close connection
between the Dehn functions and the computational complexity of the word
problem.
integer
matrices) while the Dehn function is exponential [11]. One of our
main goals is to show that still there exists a very close connection
between the Dehn functions and the computational complexity of the word
problem.
If
![]() and
and
![]() are finitely
presented, one can also define the area function of G in H. This
function is defined on the set W of all words in the alphabet X which
are equal to 1 in G. It takes every word from W to the area of this
word in H.
are finitely
presented, one can also define the area function of G in H. This
function is defined on the set W of all words in the alphabet X which
are equal to 1 in G. It takes every word from W to the area of this
word in H.
Other important concepts are the distortion function and the
length function. Let
![]() be a finitely
generated subgroup of a finitely generated group
be a finitely
generated subgroup of a finitely generated group
![]() .
Then
the distortion function
.
Then
the distortion function
![]() takes every natural
number n to
takes every natural
number n to
![]() .
In other words, in
order to compute
dG,H(n) we consider all (finitely many) elements of
G whose lengths in H are at most n, for each of these elements we
compute its length in the alphabet X, and then take the maximum of these
lengths.
.
In other words, in
order to compute
dG,H(n) we consider all (finitely many) elements of
G whose lengths in H are at most n, for each of these elements we
compute its length in the alphabet X, and then take the maximum of these
lengths.
The corresponding length function of G inside H is the function
![]() which takes every element g of G to |g|Y, the
length of g in H.
which takes every element g of G to |g|Y, the
length of g in H.
Two functions
![]() are called O-equivalent if
are called O-equivalent if
![]() for some constant c and every
for some constant c and every
![]() .
Different choices of generating sets in G and H lead to
O-equivalent length functions
.
Different choices of generating sets in G and H lead to
O-equivalent length functions
![]() and equivalent
distortion functions associated with this embedding.
and equivalent
distortion functions associated with this embedding.
If
|g|X= O(|g|Y) for every ![]() ,
or, equivalently, if the distortion
function is at most linear we say that G is quasi-isometrically
embedded into H.
Otherwise we say that G is distorted.
,
or, equivalently, if the distortion
function is at most linear we say that G is quasi-isometrically
embedded into H.
Otherwise we say that G is distorted.
For example, every subgroup of the free group is (obviously)
quasi-isometrically embedded, but the (cyclic) center
![]() of the
3-dimensional Heisenberg group
of the
3-dimensional Heisenberg group
![]() has quadratic distortion. Indeed
cn2=[an,bn] for
every n, the length of cn2 in C is n2 and the length of this
element in H3 is
has quadratic distortion. Indeed
cn2=[an,bn] for
every n, the length of cn2 in C is n2 and the length of this
element in H3 is ![]() .
.
Just as Dehn functions and isodiametric functions reflect the decidability of the word problem, the distortion function reflects the decidability of the membership problem for subgroups: if G is a finitely generated subgroup of a finitely generated group H which has solvable word problem, then the membership in G for elements of H is decidable if and only if the distortion function of G in H is recursive [12].
In this paper, we survey recent results about isoperimetric, isodiametric, length and area functions of groups obtained by the authors in collaboration with J.-C. Birget, V. Guba and E. Rips.
There are several important connections between Dehn functions and length functions. We present two connections here. The first of them plays an important role in several papers by Bridson and others on isoperimetric functions. The second connection is new.
Theorem 2 is new although a remark in [19] hints to a
possibility of some connection between distortion of subgroups in
![]() and Dehn functions. Here is a proof of this theorem. It uses the well known Mikhailova's trick (see [25]) and a result from Baumslag and Roseblade [5].
and Dehn functions. Here is a proof of this theorem. It uses the well known Mikhailova's trick (see [25]) and a result from Baumslag and Roseblade [5].
It is proved in [5] that every finitely generated subgroup E of
![]() is the equalizer (in [5] it is called the free corner pullback) of two homomorphisms
is the equalizer (in [5] it is called the free corner pullback) of two homomorphisms
![]() and
and
![]() of two finitely generated subgroups E', E'' of F2onto a finitely presented group G, that is
of two finitely generated subgroups E', E'' of F2onto a finitely presented group G, that is
![]() .
Since every finitely generated subgroup of F2 is quasi-isometrically embedded in F2,
.
Since every finitely generated subgroup of F2 is quasi-isometrically embedded in F2,
![]() is quasi-isometrically embedded into
is quasi-isometrically embedded into
![]() .
So it is enough to show that
the distortion function of the equalizer of two homomorphisms
.
So it is enough to show that
the distortion function of the equalizer of two homomorphisms
![]() and
and
![]() of two free groups onto a finitely presented group G in
of two free groups onto a finitely presented group G in
![]() is equivalent to the Dehn function of G.
is equivalent to the Dehn function of G.
Let d(k) be the Dehn function of G. Let
![]() ,
,
![]() (we assume that these generating sets are closed under taking inverses). As a
generating set for
(we assume that these generating sets are closed under taking inverses). As a
generating set for
![]() we take the set of all pairs (xi,1), (1,yj).
Let E be the equalizer of
we take the set of all pairs (xi,1), (1,yj).
Let E be the equalizer of ![]() and
and ![]() in H.
in H.
Let
![]() be generators of the kernel of
be generators of the kernel of ![]() (as a normal
subgroup of Fn). Without loss of generality we assume that the set
(as a normal
subgroup of Fn). Without loss of generality we assume that the set
![]() is closed under cyclic shifts and inverses.
is closed under cyclic shifts and inverses.
For every i=1,...,m pick one word
![]() such that
such that
![]() .
For every j=1,...,n pick one word
sj such that
.
For every j=1,...,n pick one word
sj such that
![]() .
Then the equalizer E is
generated by the pairs
(xi,ti), (sj, yj), (1,rk), i=1,...,m,
j=1,...,n,
.
Then the equalizer E is
generated by the pairs
(xi,ti), (sj, yj), (1,rk), i=1,...,m,
j=1,...,n,
![]() .
Indeed, if
.
Indeed, if
![]() ,
that is
,
that is
![]() and
u=xi1xi2...xip then
and
u=xi1xi2...xip then
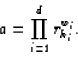
We shall prove that the distortion function of E in H is equivalent to d(k). In order to do that we need the following general statement.
Proof. If ![]() has an internal edge (i.e. an edge which belongs to
the contours of two cells) then it has an internal edge f one of whose
vertices belongs to the boundary. Let us cut
has an internal edge (i.e. an edge which belongs to
the contours of two cells) then it has an internal edge f one of whose
vertices belongs to the boundary. Let us cut ![]() along f leaving the
second vertex of f untouched. We can repeat this operation until we get a
diagram
along f leaving the
second vertex of f untouched. We can repeat this operation until we get a
diagram ![]() which does not have internal edges. It is easy to see
that the boundary label of
which does not have internal edges. It is easy to see
that the boundary label of ![]() is equal to w in the free group. The
number of edges of
is equal to w in the free group. The
number of edges of ![]() which do not belong to contours of cells (let us call
them edges of type 1) is the
same as the number of such edges in
which do not belong to contours of cells (let us call
them edges of type 1) is the
same as the number of such edges in ![]() and the
number of edges which belong
to contours of cells in
and the
number of edges which belong
to contours of cells in ![]() (edges of type 2)
is at most twice the number of such edges of
(edges of type 2)
is at most twice the number of such edges of
![]() (we cut each edge from a contour of a cell
at most once, after the cut we get two external
edges instead of one internal edge).
(we cut each edge from a contour of a cell
at most once, after the cut we get two external
edges instead of one internal edge).
Suppose that a cell ![]() in
in ![]() has more
than one edge which has a
common vertex with
has more
than one edge which has a
common vertex with ![]() but does not belong to the contour of
but does not belong to the contour of ![]() .
Take any point O on
.
Take any point O on
![]() .
Let p be the boundary path of
.
Let p be the boundary path of ![]() starting at O and let q be the boundary path of
starting at O and let q be the boundary path of ![]() starting at O.
Consider the path qq-1p. The subpath q-1p bounds a subdiagram of
starting at O.
Consider the path qq-1p. The subpath q-1p bounds a subdiagram of
![]() containing all cells but
containing all cells but ![]() .
Replace the path q in qq-1pby a loop q' with the same label starting at O and lying inside the
cell
.
Replace the path q in qq-1pby a loop q' with the same label starting at O and lying inside the
cell ![]() .
Let the region inside q' be a new cell
.
Let the region inside q' be a new cell ![]() .
Then the path
q'q-1p bounds a diagram whose boundary label is freely equal to w.
Notice that
.
Then the path
q'q-1p bounds a diagram whose boundary label is freely equal to w.
Notice that ![]() has exactly one edge having a common vertex with
has exactly one edge having a common vertex with ![]() and not belonging to the contour of
and not belonging to the contour of ![]() .
Thus this operation reduces
the number of cells which have more
than one edge which has a
common vertex with the cell but does not belong to the contour of it.
.
Thus this operation reduces
the number of cells which have more
than one edge which has a
common vertex with the cell but does not belong to the contour of it.
After a number of such transformations we shall have a diagram ![]() which has the form of a tree T with cells hanging like leaves (each has exactly one common vertex with the tree).
which has the form of a tree T with cells hanging like leaves (each has exactly one common vertex with the tree).
The number of
edges of type 1 in ![]() cannot be bigger
than the number of all edges in
cannot be bigger
than the number of all edges in ![]() ,
so it cannot be more
than two times
bigger than the total number of edges in
,
so it cannot be more
than two times
bigger than the total number of edges in ![]() .
.
The boundary label of ![]() is freely equal to w, and it has the form
u1ri1u2ri2...udridud+1 where d is the number of cells
in
is freely equal to w, and it has the form
u1ri1u2ri2...udridud+1 where d is the number of cells
in ![]() ,
u1u2...ud+1 is the label of a tree, so
u1u2...ud+1=1 in the free group. The sum of lengths
of ui is
at most four times the number of edges in
,
u1u2...ud+1 is the label of a tree, so
u1u2...ud+1=1 in the free group. The sum of lengths
of ui is
at most four times the number of edges in ![]() because
the word
u1u2...ud+1 is written on the tree T, and when we
travel along the tree, we pass through each edge twice.
because
the word
u1u2...ud+1 is written on the tree T, and when we
travel along the tree, we pass through each edge twice.
The lemma is proved.
Let us consider the distortion function of E in H.
Without loss of generality we can assume that d(k) is the Dehn function of the presentation
![]() (recall that Dehn functions of different finite presentations of the same group are equivalent).
(recall that Dehn functions of different finite presentations of the same group are equivalent).
Let (u,v) be any element in E whose length in H, |u|+|v|, is ![]() .
Then as before
.
Then as before
Notice that the length of the word adoes not exceed
Let ![]() be the minimal area van Kampen diagram over the presentation
be the minimal area van Kampen diagram over the presentation
By Lemma 1,
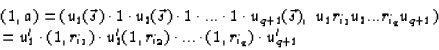
This implies that the distortion function of E in H does not exceed a function equivalent to the Dehn function d.
To prove that the Dehn function ddoes not exceed a function equivalent to the distortion
function of E in H, it is enough, for every number ![]() ,
to take a word
,
to take a word ![]() ,
from the kernel of
,
from the kernel of ![]() ,
,
![]() ,
of area d(p). Then it is easy to
see that
any representation of (1,a) as a product of generators of
E must contain at least d(p) factors of the form (1,rk) (because it corresponds to a
representation of a in the form
u1ri1u2ri2...ridud+1 where
u1...ud+1=1 in the free group).
,
of area d(p). Then it is easy to
see that
any representation of (1,a) as a product of generators of
E must contain at least d(p) factors of the form (1,rk) (because it corresponds to a
representation of a in the form
u1ri1u2ri2...ridud+1 where
u1...ud+1=1 in the free group).
![]()