Dr. Mark V. Sapir

• List of concepts and their definitions
• Chapter 1. Systems of linear equations
  1. Systems of linear equations
  2. The geometric meaning of systems of linear equations
  3. Augmented matrices
  4. The Gauss-Jordan elimination algorithm
  5. The theorem about solutions of systems of linear equations.
  6. Homogeneous systems of equations
  7. The theorem about solutions of homogeneous systems of equations.
• Chapter 2. Matrices
  1. Matrix operations
  2. Properties of matrix operations
  3. Properties that do not hold
  4. Transpose, trace, inverse
  5. The theorem about transposes
  6. The theorem about traces
  7. The first theorem about inverses
  8. Elementary matrices
  9. The theorem about the product EA where E is an elementary matrix
  10. The lemma about inverses of elementary matrices
  11. The second theorem about inverses. An algorithm of finding the inverse matrix.
  12. Symmetric, diagonal, triangular matrices.
  13. The first theorem about symmetric matrices.
  14. The second theorem about symmetric matrices.
  15. The third theorem about symmetric matrices.
  16. The theorem about triangular matrices.
  17. The theorem about skew-symmetric matrices
• Chapter 3. Determinants
  1. Determinants.
  2. The theorem about the sign of a permutation.
  3. The first theorem about determinants.
  4. The second theorem about determinants.
  5. The third theorem about determinants.
  6. Corollaries from the theorems about determinants.
  7. Cramer's rule.
• Chapter 4. Linear and Euclidean vector spaces
  1. Linear and Euclidean Spaces.
  2. Theorem about norms.
  3. Theorem about distances.
  4. Pythagoras theorem.
• Chapter 5. Linear transformations
  1. Linear transformations from Rⁿ to R^m
  2. A characterization of linear transformations from R^m to Rⁿ
  3. Every linear transformation from R^m to Rⁿ takes 0 to 0
  4. Linear operators in R²
  5. Operations on linear operators
  6. Theorem about products, sums and scalar multiples of linear transformations.
  7. The theorem about invertible linear operators and invertible matrices.
  8. The theorem about invertible, injective and surjective linear operators
  9. Linear transformations of arbitrary vector spaces
  10. The theorem about linear transformations of arbitrary vector spaces.
• Chapter 6. Subspaces
  1. Subspaces of vector spaces.
  2. The theorem about subspaces.
  3. Sources of subspaces: kernels and ranges of linear transformations"
  4. Theorem: kernels and ranges are subspaces.
  5. Theorem: the set of solutions of a homogeneous system of equations is a subspace.
  6. Sources of subspaces: subspaces spanned by vectors
  7. Linearly independent sets of vectors
  8. Theorem: when a set and its subset span the same subspace?
  9. The theorem about linearly independent sets of elements in a vector space.
  10. The theorem about linearly dependent sets of elements in a vector space.
  11. The theorem about linearly independent sets of functions (the theorem about Wronskian)
  12. Basis and dimension
  13. The theorem about bases
  14. The theorem about dimension
  15. The theorem about the rank of a matrix
  16. The theorem about the core of a set of vectors in Rⁿ
  17. The theorem about dimensions of the range and the kernel of a linear transformation from R^m to Rⁿ
  18. Orthogonal complements, orthogonal bases
  19. The theorem about orthogonal complements
  20. Orthogonal complements in Rⁿ and systems of linear equations
  21. Theorem: the orthogonal complement of V in Rⁿ is the set of solutions of a system of homogeneous linear equatins
  22. Orthogonal bases. The Gram-Schmidt algorithm
  23. The Gram-Schmidt algorithm
  24. Theorem: every orthogonal set of vectors is linearly independent.
  25. Proof of the theorem about orthogonal complements.
  26. Projections on subspaces, distance from a vector to a subspace
  27. The theorem about distances between vectors and subspaces.
  28. Applications to systems of linear equations. Least squares solutions
  29. The procedure of finding a least squares solution of a system of linear equations
  30. An alternative procedure of finding a least squares solution of a system of linear equations
  31. Change of basis in a vector space
  32. Matrices of linear operators in finite dimensional vector spaces
  33. The theorem about matrices of linear operators in finite dimensional vector spaces
  34. Matrices of linear operators in different bases
  35. Matrices of the same operator in different bases are similar
  36. Eigenvectors and eigenvalues
  37. How to find eigenvectors and eigenvalues

Systems of linear equations

A linear equation is an equation of the form

               a1x1+a2x2+...+anxn=b             (1)

where x₁,...,x_n are unknowns, a₁,...,a_n,b are coefficients.

Example:

          3x-4y+5z=6                                   (2)

This equation has three unknowns and four coefficients (3, -4, 5, 6).

A solution of a linear equation (1) is a sequence of numbers x₁,...,x_n which make (1) a true equality.

Example:

       x=2, y=0, z=0

is a solution of equation (2).

A linear equation can have infinitely many solutions, exactly one solution or no solutions at all.

Equation (2) has infinitely many solutions. To find them all we can set arbitrary values of x and y and then solve (2) for z.

We get:

				               x = s
				               y = t
				               z = (6-3s+4t)/5

These formulas give all solutions of our equation meaning that for every choice of values of t and s we get a solution and every solution is obtained this way. Thus this is a (the) general solution of our equation.

There may be many formulas giving all solutions of a given equation. For example Maple gives another formula:
> with(linalg);

This command starts the linear algebra package.
> A:=matrix(1,3,[3,-4,5]):b:=vector([6]):linsolve(A, b);

This command asks Maple to solve the system of equations.

The solution has two parameters t₁ and t₂;

In order to get this solution "by hand" one can give y and z arbitrary values (t₁ and t₂) and solve for x.

A system of linear equations is any sequence of linear equations. A solution of a system of linear equations is any common solution of these equations. A system is called consistent if it has a solution. A general solution of a system of linear equations is a formula which gives all solutions for different values of parameters.

Examples. 1. Consider the system:

				          x +  y =  7
				         2x + 4y = 18

This system has just one solution: x=5, y=2. This is a general solution of the system.

2. Consider the system:

				       x +  y + z =  7
				      2x + 4y + z = 18.

This system has infinitely many solutions given by this formula:

				        x = 5 - 3s/2
				        y = 2 + s/2
				        z = s

This is a general solution of our system.

In order to find a general solution of a system of equations, one needs to simplify it as much as possible. The simplest system of linear equations is

					        x = a
					        y = b
					        .....

where every equation has only one unknown and all these unknowns are different. It is not possible to reduce every system of linear equations to this form, but we can get very close. There are three operations that one can apply to any system of linear equations:

1. Replace an equation by the sum of this equation and another equation multiplied by a number.
2. Swap two equations.
3. Multiply an equation by a non-zero number.

The system obtained after each of these operations is equivalent to the original system, meaning that they have the same solutions.

For example consider the system

				         x +  y =  7
				        2x + 4y = 18

We can first replace the second equation by the second equation plus the first equation multiplied by -2. We get

				          x + y = 7
				             2y = 4

Now we can use the third operation and multiply the second equation by 1/2:

				          x + y = 7
  				              y = 2

Finally we can replace the first equation by the sum of the first equation and the second equation multiplied by -1:

					        x = 5
					        y = 2

Since this system is equivalent to the original system, we get that x=5, y=2 is the general solution of the original system.

The geometric meaning of systems of linear equations

Consider an (x,y)-plane and the set of points satisfying ax+by=c. This set of points is either a line (if a or b is not 0) or the whole plane (if a=b=c=0), or empty (if a=b=0 but c is not 0).

The set of solutions of the system

			                ax +  by = c
			               a'x + b'y = c'

 

is the intersection of the sets of solutions of the individual equations. For example if these equations define lines on the plane, the intersection may be a point -- if the lines are not parallel, a line -- if the lines coincide, or empty -- if the lines are parallel.

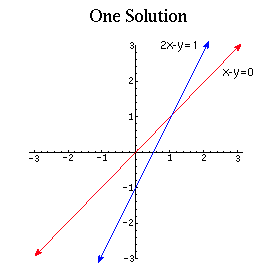
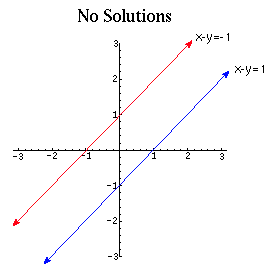
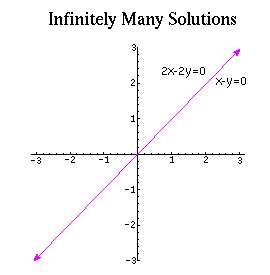
A system of equations in 3 or more variables has similar geometric meaning.

Augmented matrices.

Consider the following problem:

Given the system of equations

	                  x + y + 2z = a
	                  x +      z = b                        (1)
	                 2x + y + 3z = c,
  

show that it has a solution only if a+b=c.

In order to prove that, replace the first equation by the sum of the first two equations:

			                 2x + y + 3z = a + b
			                  x +      z = b
			                 2x + y + 3z = c

This system is equivalent to the previous one, so it has a solution if and only if the initial system has a solution. But comparing the first and the third equations of this system we notice that it has a solution only if a+b=c. The problem is solved.

Now suppose that we have that a+b=c and we want to find the general solution of this system.

Then we need to simplify the system by using three operations (adding, swapping, multiplying). It is more convenient to work not with the system but with its augmented matrix, the array (table, matrix) consisting of the coefficients of the left sides of the equations and the right sides. For example the system (1) from the problem that we just solved has the following augmented matrix:

The number of equations in a system of linear equations is equal to the number of rows in the augmented matrix, the number of unknowns is equal to the number of columns minus 1, the last column consists of the right sides of the equations.

When we execute the operations on the systems of equations, the augmented matrix changes. If we add equation i to equation j, then row i will be added to row j, if we swap equations, the corresponding rows get swapped, if we multiply an equation by a (non-zero) number, the corresponding row is multiplied by this number.

Thus, in order to simplify a system of equations it is enough to simplify its augmented matrix by using the following row operations:

1. Replace a row by this row plus another row multiplied by a number.
   
2. Swap two rows.
   
3. Multiply a row by a non-zero number.
   

For example let us simplify the augmented matrix of the system (1) from the problem that we just solved.

First we replace the first row by the sum of the first and the second rows:

Then we subtract the first row from the third row (remember that a+b=c):

Then we subtract the second row multiplied by 2 from the first row. :

Then we swap the first two rows and obtain the following matrix

The last matrix has several important features:

1. All zero rows (rows consisting of zeroes) are at the buttom.
2. Every non-zero row starts with several zeroes followed by 1. This 1 is called the leading 1 of the row.
3. The position of the leading 1 in the row with bigger number is further to the right than for the row with smaller number.
4. Every number below the leading 1 is zero.
5. Every number above the leading 1 is zero.

A matrix which satisfies the first four conditions is called a matrix in the row echelon form or a row echelon matrix.

A matrix which satisfies all five conditions is called a matrix in the reduced row echelon form or a reduced row echelon matrix.

It is very easy to find the general solution of a system of linear equations whose augmented matrix has the reduced row echelon form.

Consider the system of equations corresponding to the last matrix that we got:

			               x +     z = b
			                   y + z = a - b

The unknowns corresponding to the leading 1's in the row echelon augmented matrix are called leading unknowns. In our case the leading 1's are in the first and the second positions, so the leading unknowns are x and y. Other unknowns are called free.

In our case we have only one free unknown, z. If we move it to the right and denote it by t, we get the following formulas:

			               x = b - t
			               y = a - b - t
			               z = t

This system gives us the general solution of the original system with parameter t. Indeed, giving t arbitrary values, we can compute x, y and z and obtain all solutions of the original system of equations.

Similarly, we can get a general solution of every system of equations whose matrix is in the reduced row echelon form:

One just has to move all free variables to the right side of the equations and consider them as parameters.

Example Consider the system of equations:

                         x1 + 2x2 +         x4   =  6
                                      x3 +  6x4  =  7
                                                 x5=1

Its augmented matrix is

The matrix has the reduced row echelon form. The leading unknowns are x₁, x₃ and x₅; the free unknowns are x₂ and x₄. So the general solution is:

	                      x1= 6-2t-s
	                      x2= s
	                      x3= 7-6t
	                      x4= t
	                      x5= 1

If the augmented matrix does not have the reduced row echelon form but has the (ordinary) row echelon form then the general solution also can be easily found.

The method of finding the solution is called the back-substitution.

First we solve each of the equations for the leading unknowns The last non-zero equation gives us the expression for the last leading unknown in terms of the free unknowns. Then we substitute this leading unknown in all other equations by this expression. After that we are able to find an expression for the next to the last leading unknown, replace this unknown everywhere by this expression, etc. until we get expressions for all leading unknowns. The expressions for leading unknowns that we find in this process form the general solution of our system of equations.

Example. Consider the following system of equations.

                      x1-3x2+ x3-x4 = 2
                          x2+2x3-x4 = 3
                              x3+x4 = 1

Its augmented matrix

is in the row echelon form.

The leading unknowns are x₁, x₂, x₃; the free unknown is x₄.

Solving each equation for the leading unknown we get:

	                    x1=2+3x2-x3+x4
	                    x2=3-2x3+x4
	                    x3=1-x4

The last equation gives us an expression for x₃: x₃=1-x₄. Substituting this into the first and the second equations gives:

                    x1=2+3x2-1+x4+x4=1+3x2+2x4
                    x2=3-2(1-x4)+x4=1+3x4
                    x3=1-x4

                    x1=1+3(1+3x4)+2x4=4+11 x4
                    x2=1+3x4
                    x3=1-x4

Now we can write the general solution:

		                    x1=4+11 s
		                    x2=1+ 3 s
		                    x3=1-   s
		                    x4=     s

Let us check if we made any arithmetic mistakes. Take x₄=1 and compute x₁=15, x₂=4, x₃=0, x₄=1. Substitute it into the original system of equations:

	                    15 - 3 * 4 + 0 - 1 = 2
	                         4 + 2 * 0 - 1 = 3
	                                 0 + 1 = 1

OK, it seems that our solution is correct.

The Gauss-Jordan elimination procedure

There exists a standard procedure to obtain a reduced row echelon matrix from a given matrix by using the row operations.

This procedure consists of the following steps.

1. Locate the leftmost column which does not consist of zeroes.
2. If necessary swap the first row with the row which contains a non-zero number a in the column found on step 1.
3. If this number a is not 0, multiply the first row by 1/a, to get a leading 1 in the first row.
4. Use the first row to make zeroes below the leading 1 in the first row (by using the adding operation).
5. Cover the first row and apply the first 4 steps to the remaining sub-matrix. Continue until the whole matrix is in the row echelon form.
6. Use the last non-zero row to make zeroes above the leading 1 in this row. Use the second to last non-zero row to make zeroes above the leading 1 in this row. Continue until the matrix is in the reduced row echelon form.

Example

Theorem. A system of linear equations either has no solutions or has exactly one solution or has infinitely many solutions. A system of linear equations has infinitely many solutions if and only if its reduced row echelon form has free unknowns and the last column of the reduced row echelon form has no leading 1's. It has exactly one solution if and only if the reduced row echelon form has no free unknowns and the last column of the reduced row echelon form has no leading 1. It has no solutions if and only if the last column of the reduced row echelon form has a leading 1.

Homogeneous systems

A system of linear equation is called homogeneous if the right sides are equal to 0.

Example:

			              2x + 3y - 4z = 0
			               x -  y +  z = 0
			               x -  y      = 0

A homogeneous system of equations always has a solution (0,0,...,0). Therefore the theorem about solutions of systems of linear equations implies the first part of the following result.

Theorem. Every homogeneous system has either exactly one solution or infinitely many solutions. If a homogeneous system has more unknowns than equations, then it has infinitely many solutions.

Matrices and matrix operations

A matrix is a rectangular array of numbers. The numbers in the array are called entries.

Examples. Here are three matrices:

The size of a matrix is the pair of numbers: the number of rows and the number of columns. The matrices above have sizes (2,3), (1,4), (2,1), respectively.

A matrix with one row is called a row-vector. A matrix with one column is called a column-vector. In the example above the second matrix is a row-vector, the third one is a column-vector. The entry of a matrix A which stays in the i-th row and j-th column will be usually denoted by A_ij or A(i,j).

A matrix with n rows and n columns is called a square matrix of size n.

Discussing matrices, we shall call numbers scalars. In some cases one can view scalars as 1x1-matrices.

Matrices were introduced first in the middle of 19-th century by W. Hamilton and A. Cayley. Following Cayley, we are going to describe an arithmetic where the role of numbers is played by matrices.

Motivation.

In order to solve an equation

with a not equal 0 we just divide b by a and get x. We want to solve systems of linear equations in a similar manner. Instead of the scalar a we shall have a matrix of coefficients of the system of equations, that is the array of the coefficients of the unknowns (i.e. the augmented matrix without the last column). Instead of x we shall have a vector of unknowns and instead of b we shall have the vector of right sides of the system.

In order to do that we must learn how to multiply and divide matrices.

But first we need to learn when two matrices are equal, how to add two matrices and how to multiply a matrix by a scalar.

Two matrices are called equal if they have the same size and their corresponding entries are equal.
The sum of two matrices A and B of the same size (m,n) is the matrix C of size (m,n) such that C(i,j)=A(i,j)+B(i,j) for every i and j.

Example.

In order to multiply a matrix by a scalar, one has to multiply all entries of the matrix by this scalar.

Example:

The product of a row-vector v of size (1, n) and a column vector u of size (n,1) is the sum of products of corresponding entries: uv=u(1)v(1)+u(2)v(2)+...+u(n)v(n)

Example:

                        [ 3 ]
            [1, 2, 3] * [ 4 ] =1*3 + 2*4 + 3*1 = 3+8+3=14
                        [ 1 ]

Example:

                        [ x ]
            [2, 4, 3] * [ y ] = 2x + 4y + 3z
                        [ z ]

As you see, we can represent the left side of a linear equation as a product of two matrices. The product of arbitrary two matrices which we shall define next will allow us to represent the left side of any system of equations as a product of two matrices.

Let A be a matrix of size (m,n), let B be a matrix of size (n,k) (that is the number of columns in A is equal to the number of rows in B. We can subdivide A into a column of m row-vectors of size (1,n). We can also subdivide B into a row of k column-vectors of size (n,1):

          r1
          r2
       A =...      B=[c1 c2 ... ck]
          rm

(C(i,j) is the product of the row-vector r_i and the column-vector c_j).

Matrices A and B such that the number of columns of A is not equal to the number of rows of B cannot be multiplied.

Example:

Example:

You see: we can represent the left part of a system of linear equations as a product of a matrix and a column-vector. The whole system of linear equations can thus be written in the following form:

where A is the matrix of coefficients of the system -- the array of coefficients of the left side (do not mix with the augmented matrix), v is the column-vector of unknowns, b is the column vector of the right sides (constants).

Properties of matrix operations.

1. The addition is commutative and associative: A+B=B+A, A+(B+C)=(A+B)+C
2. The product is associative: A(BC)=(AB)C
3. The product is distributive with respect to the addition: A(B+C)=AB+AC, (A+B)C=AC+BC
4. The multiplication by scalar is distributive with respect to the addition of matrices: a(B+C)=aB+aC
5. The product by a scalar is distributive with respect to the addition of scalars: (a+b)C=aC+bC
6. a(bC)=(ab)C; a(BC)=(aB)C; (Ab)C=A(bC)
7. 1 A=A; 0 A=0 (here the 0 on the left is the number zero, the 0 on the right is the zero matrix of the same size as A, that is a matrix all of whose entries are 0
8. 0+A=A+0=A (here 0 is the zero matrix of the same size as A).
9. 0A=0 (these two zeroes are matrices of appropriate sizes).
10. Let I_n denote the identity matrix of order n that is a square matrix of order n with 1s on the main diagonal and zeroes everywhere else. Then for every m by n matrix A the product of A and I_n is A and the product of I_m and A is A.

Example

The following properties of matrix operations do not hold:

1. For every square matrices A and B we have AB=BA:

   Example:

   A =

   [ 1 2 ] [ 0 1 ]

   ,

   B =

   [ 1 0 ] [ 2 1 ]

   Indeed,

   AB =

   [ 5 2 ] [ 2 1 ]

   ,

   BA =

   [ 1 2 ] [ 2 5 ]

2. For every matrices A, B, C, if AB=AC and A is not a zero matrix then B=C.
   

   Example:

   A =

   [ 1 0 ] [ 0 0 ]

   ,

   B =

   [ 0 0 ] [ 1 0 ]

   ,

   C =

   [ 0 0 ] [ 0 1 ]

   Then AB=AC=0 but B and C are not equal. Notice that this example shows also that a product of two non-zero matrices can be zero.

Transpose, trace, inverse

There are three other important operations on matrices.

If A is any m by n matrix then the transpose of A, denoted by A^T, is defined to be the n by m matrix obtained by interchanging the rows and columns of A, that is the first column of A^T is the first row of A, the second column of A^T is the second row of A, etc.

Example.
The transpose of

If A is a square matrix of size n then the sum of the entries on the main diagonal of A is called the trace of A and is denoted by tr(A).

Example.
The trace of the matrix

A square matrix of size n A is called invertible if there exists a square matrix B of the same size such that AB = BA = I_n, the identity matrix of size n. In this case B is called the inverse of A.

Examples. 1. The matrix I_n is invertible. The inverse matrix is I_n: I_n times I_n is I_n because I_n is the identity matrix.

2. The matrix A

is invertible. Indeed the following matrix B:

is the inverse of A since A*B=I₂=B*A.

3. The zero matrix O is not invertible. Indeed, if O*B=I_n then O=O*B=I_n which is impossible.

4. A matrix A with a zero row cannot be invertible because in this case for every matrix B the product A*B will have a zero row but I_n does not have zero rows.

5. The following matrix A:

is not invertible. Indeed, suppose that there exists a matrix B:

such that A*B=I₃. The corresponding entries of A*B and I₃ must be equal, so we get the following system of nine linear equations with nine unknowns:

This system does not have a solution which can be shown with the help of Maple.

Now we are going to prove some theorems about transposes, traces and inverses.

Theorem. The following properties hold:

1. (A^T)^T=A, that is the transpose of the transpose of A is A (the operation of taking the transpose is an involution).
2. (A+B)^T=A^T+B^T, the transpose of a sum is the sum of transposes.
3. (kA)^T=kA^T.
4. (AB)^T=B^TA^T, the transpose of a product is the product of the transposes in the reverse order.

Theorem. The following properties of traces hold:

1. tr(A+B)=tr(A)+tr(B)
2. tr(kA)=k tr(A)
3. tr(A^T)=tr(A)
4. tr(AB)=tr(BA)

Theorem. The following properties hold:

1. If B and C are inverses of A then B=C. Thus we can speak about the inverse of a matrix A, A^-1.
2. If A is invertible and k is a non-zero scalar then kA is invertible and (kA)^-1=1/k A^-1.
3. If A and B are invertible then AB is invertible and

   (AB)^-1=B^-1 A^-1

   that is the inverse of the product is the product of inverses in the opposite order. In particular

   (Aⁿ)^-1=(A^-1)ⁿ.

4. (A^T)^-1=(A^-1)^T, the inverse of the transpose is the transpose of the inverse.
5. If A is invertible then (A^-1)^-1=A.

The proofs of 2, 4, 5 are left as exercises.

---

Notice that using inverses we can solve some systems of linear equations just in the same way we solve the equation ax=b where a and b are numbers. Suppose that we have a system of linear equations with n equations and n unknowns. Then as we know, this system can be represented in the form Av=b where A is the matrix of the system, v is the column-vector of unknowns, b is the column-vector of the right sides of the equations. The matrix A is a square matrix. Suppose that it has an inverse A^-1. Then we can multiply both sides of the equation A v = b by A^-1 on the left. Using the associativity, the fact that A^-1 A=I and the fact that Iv=v, we get: v=A^-1b. This is the solution of our system.

---

---