The Linear Logo

Dr. Mark V. Sapir

Linear Transformations From Rn to Rm


There is a yet another way to look at systems of linear equations. Suppose that we want to find all solutions of the following system of linear equations

Av=b

where A is an m by n matrix of coefficients and b is the column of right sides. For every n-vector v we can get an m-vector Av. Our goal is to find all n-vectors v such that this m-vector is b. Thus we have a function which takes any vector v from Rn to the vector Av from Rm and our goal is to find all values of the argument of this function for which the function has a particular value.

A function from Rn to Rm which takes every n-vector v to the m-vector Av where A is a m by n matrix, is called a linear transformation. The matrix A is called the standard matrix of this transformation. If n=m then the transformation is called a linear operator of the vector space Rn.

Notice that by the definition the linear transformation with a standard matrix A takes every vector

(x1,...,xn)

from Rn to the vector

(A(1,1)x1+...+A(1,n)xn, A(2,1)x1+...+A(2,n)xn,...,A(m,1)x1+...+A(m,n)xn)

from Rm where A(i,j) are the entries of A. Conversely, every transformation from Rn to Rm given by a formula of this kind is a linear transformation and the coefficients A(i,j) form the standard matrix of this transformation.

Examples. 1. Consider the transformation of R2 which takes each vector (a,b) to the opposite vector (-a,-b). This is a linear operator with standard matrix

[ -1 0 ]
[ 0 -1 ]

2. More generally, the dilation operator is the linear operator from Rn to Rn which takes every vector

(x1,...,xn)

to

(kx1,...,kxn)

where k is a constant.

3. If we take a vector (x,y) in R2 and reflect it about the x-axis, we get vector (x,-y). Clearly, this reflection is a linear operator. Its standard matrix is

[ 1 0 ]
[ 0 -1 ]

4. If we project a vector (x,y) on the x-axis, we get vector (x,0). This projection is also a linear operator. Its standard matrix is

[ 1 0 ]
[ 0 0 ]

5. If we rotate a vector (x,y) through 90 degrees counterclockwise, we get vector (-y, x). This rotation is a linear operator with standard matrix

[ 0 -1 ]
[ 1 0 ]


A characterization of linear transformations

We shall prove that reflections about arbitrary lines, projections on arbitrary axes, and rotations through arbitrary angles in R2 are linear operators. In order to do this we need the following simple characterization of linear transformations from Rn to Rn.

Theorem. A function T from Rn to Rm is a linear transformation if and only if it satisfies the following two properties:

  1. For every two vectors A and B in Rn

    T(A+B)=T(A)+T(B);

  2. For every vector A in Rn and every number k

    T(kA)=kT(A).


Proof


This proof shows that if T is a linear transformation, Vi (I=1,...,n) is the vector with I-th coordinate 1 and other coordinates 0, then T(Vi) is the I-th column in the standard matrix of T. This provides us with a way to find the standard matrix of a linear transformation.
Notice that in R3, vectors V1, V2, V3 are the basic vectors i, j, k. So we shall call Vi the basic vectors in Rn. We shall give a general definition of bases in Rn and other vector spaces later.

As a corollary of the characterization of linear transformations from Rm to Rn we can deduce the following statement.

Corollary. Every linear transformation T from Rm to Rn takes 0 of Rm to 0 of Rn.

Indeed, take k=0 and an arbitrary vector A then

T(0)=T(0*A)=0T(A)=0.

Here we used the second condition of the characterization.

Linear operators in R2

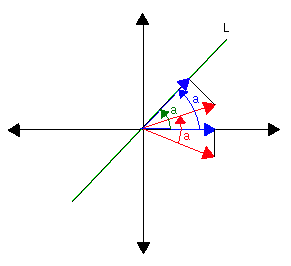
Example 1. Projection on an arbitrary line in R2. Let L be an arbitrary line in R2. Let TL be the transformation of R2 which takes every 2-vector to its projection on L. It is clear that the projection of the sum of two vectors is the sum of the projections of these vectors. If we multiply a vector by a scalar then its projection will also be multiplied by this scalar. Thus by the characterization of linear transformations, TL is a linear operator on R2.

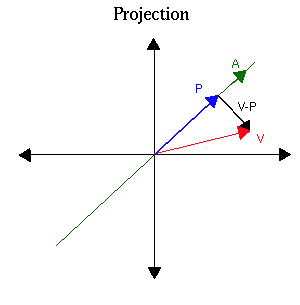
Image of Projection Composite

Let us find the standard matrix of the projection on the line y=kx. This line has the direction of the vector A=(1,k). Let V be an arbitrary vector (x,y) in R2. Then the projection P is such a vector that

  1. P is parallel to A, that is P=tA=(t, kt);
  2. V-P is perpendicular to A. This means that <(V-P),A>=0 or

    <(x-t, y-kt)*(1,k)>=x-t+k(y-kt)=0

From this, we can deduce that

t=(x+ky)/(1+k2)

So

P=((x+ky)/(1+k2), k(x+ky)/(1+k2))

Therefore the standard matrix of the projection is

1/(k2+1) [ 1 k ]
[ k k2 ]

Notice that the formula for vector P gives another proof that the projection is a linear operator (compare with the general form of linear operators).

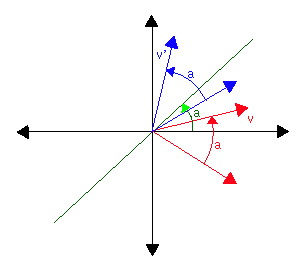
Example 2. Reflection about an arbitrary line.

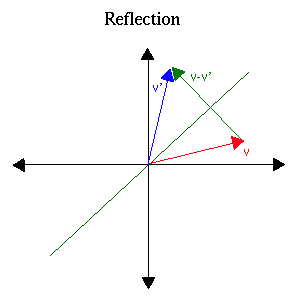
Image of Reflection

If P is the projection of vector v on the line L then V-P is perpendicular to L and Q=V-2(V-P) is equal to the reflection of V about the line L. Thus Q=2P-V. Using the formula for P that we have, we can deduce a formula for Q:

P=((x+ky)/(1+k2), k(x+ky)/(1+k2),

Q=2P-V=(2(x+ky)/(1+k2)-x, 2k(x+ky)/(1+k2)-y).

This gives us the standard matrix of the reflection:

1/(k2+1) [ 1-k2 2k ]
[ 2k k2-1 ]

Example 3. Rotation through angle a

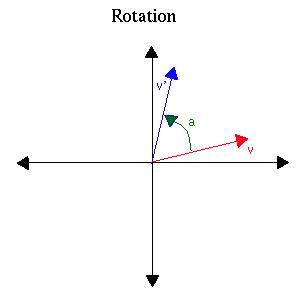
Image of Reflection

Using the characterization of linear transformations it is easy to show that the rotation of vectors in R2 through any angle a (counterclockwise) is a linear operator. In order to find its standard matrix, we shall use the observation made immediately after the proof of the characterization of linear transformations. This observation says that the columns of the standard matrix are images of the basic vectors (1,0) and (0,1). It is clear that these images are (cos(a), sin(a)) and (-sin(a), cos(a)). Therefore the standard matrix of the rotation is:


[ cos(a) -sin(a) ]
[ sin(a) cos(a) ]

Notice that the rotation clockwise by angle a has the following matrix:


[ cos(a) sin (a) ]
[ -sin(a) cos(a) ]

because it is equal to the rotation counterclockwise through the angle -a.

Operations on linear transformations

Suppose that T is a linear transformation from Rm to Rn with standard matrix A and S is a linear transformation from Rn to Rk with standard matrix B. Then we can compose or multiply these two transformations and create a new transformation ST which takes vectors from Rm to Rk. This transformation first applies T and then S. Not any two transformations can be multiplied: the transformation S must start where T ends. But any two linear operators in Rn (that is linear transformations from Rn to Rn) can be multiplied.

Notice that if v is a vector in Rn then

T(V)=AV

by the definition of the standard matrix of a linear transformation. Then

ST(V)=S(T(V))=B(AV)=(BA)V

Thus the product ST is a linear transformation and the standard matrix ST is the product of standard matrices BA.

Example 1. Suppose that T and S are rotations in R2, T rotates through angle a and S rotates through angle b (all rotations are counterclockwise). Then ST is of course the rotation through angle a+b. The standard matrix of T is

[ cos(a) -sin(a) ]
[ sin(a) cos(a) ]


The standard matrix of S is
[ cos(b) -sin(b) ]
[ sin(b) cos(b) ]


Thus the standard matrix of ST must be the product of these matrices:
[ cos(a)cos(b)-sin(a)sin(b) -cos(a)sin(b)-sin(a)cos(b) ]
[ cos(a)sin(b)+sin(a)cos(b) cos(a)cos(b)-sin(a)sin(b) ]


On the other hand this is the standard matrix of the rotation through angle a+b, so its standard matrix must be equal to
[ cos(a+b) -sin(a+b) ]
[ sin(a+b) cos(a+b) ]


This gives us the well known trigonometric formulas:

cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
sin(a+b)=sin(a)cos(b)+cos(a)sin(b)


Example 2. Let L be a line which forms angle a with the x-axis. Then the reflection about L can be represented as a product of three operators:
  1. The rotation through a clockwise.
  2. The reflection about the x-axis.
  3. The rotation through a counterclockwise.

Image of Reflection Composite

Thus we could find the standard matrix of the reflection about the line L by multiplying the standard matrices of these three transformations.

Similarly, the projection on L can be decomposed into a product of three operators:

  1. The rotation through a clockwise.
  2. The projection on the x-axis.
  3. The rotation through a counterclockwise.

Image of Projection Composite

If T and S are linear transformations from Rm to Rn then we can add them, that is create a function T+S also from Rm to Rn which takes every vector V to T(V)+S(V).

If A and B are the standard matrices of T and S respectively, then

(T+S)(V)=T(V)+S(V)=AV+BV=(A+B)*V


Thus the sum of linear transformations from Rm to Rn is again a linear transformation and the standard matrix of the sum of linear transformations is the sum of standard matrices of these transformations.

We can also multiply a linear transformation by a scalar. If k is a number and T is a linear transformation from Rm to Rn then kT is a function from Rm to Rn which takes every vector V from Rm to kT(V). It is easy to see that the standard matrix of kT is kA.

Summarizing the properties of linear transformations from Rm to Rn that we have obtained so far, we can formulate the following theorem.

Theorem. 1. The product ST of a linear transformation T from Rm to Rn and a linear transformation S from Rn to Rk is a linear transformation from Rm to Rk and the standard matrix of ST is equal to the product of standard matrices of S and T.

2. If T and S are linear transformations from Rm to Rn then T+S is again a linear transformation from Rm to Rn and the standard matrix of this transformation is equal to the sum of standard matrices of T and S.

3. If T is a linear transformation from Rm to Rn and k is a scalar then kT is again a linear transformation from Rm to Rn and the standard matrix of this transformation is equal to k times the standard matrix of T.

By definition, the identity function from Rn to Rn is the function which takes every vector to itself. It is clear that the identity function is a linear operator whose standard matrix is the identity matrix. Let us denote the identity operator by Id.

A linear operator T in Rn is called invertible if there exists another linear operator S in Rn such that TS=ST=Id. In this case S is called the inverse of T. By definition S undoes what T does, that is if T takes V to W then S must take W to V (otherwise ST would not be the identity operator). If A is the standard matrix of T and B is the standard matrix of S then ST has standard matrix BA. So if S is the inverse of T then BA=I. Conversely, if BA=I then the linear operator S with standard matrix B is the inverse of T because ST is the linear operator whose standard matrix is I. Thus we can conclude that the following statement is true.

Theorem. A linear operator T in Rn is invertible if and only if its standard matrix is invertible. If A is the standard matrix of T then A-1 is the standard matrix of T-1.


Example 1. The reflection about a line in R2 is invertible and the inverse of a reflection is the reflection itself (indeed, if we apply the reflection to a vector twice, we do not change the vector).


Example 2. The rotation through angle a is invertible and the inverse is the rotation through angle -a.

Example 3. The projection on a line in R2 is not invertible because there are many vectors taken by the projection to the same vector, so we cannot uniquely reconstruct a vector by its image under the projection.

Our next goal is to consider properties of invertible linear operators.

First let us recall some properties of invertible maps (functions). Let T be a map from set X into set Y. We say that T is injective or one to one if T maps different elements to different elements, that is if T(u)=T(v) then necessarily u=v. We call T surjective or onto if every element in Y is an image of some element in X that is for every y in Y there exists an x in X such that T(x)=y.

A function T from X to X is called invertible if there exists another function S from X to X such that TS=ST=Id, the identity function (that is if T takes x to y then S must take y to x). It is easy to see that T is invertible if and only if it is injective and surjective.

There exist functions which are non-injective and non-surjective (the function T(x)=x2 from R to R), non-injective and surjective (say, T(x)=x3-x from R to R), injective and non-surjective (say, T(x)=arctan(x) from R to R), injective and surjective (any invertible function, say T(x)=x3 from R to R).

Thus the following theorem about linear operators is very surprising.

Theorem. For every linear operator T in Rn with standard matrix A the following conditions are equivalent:

  1. T is invertible.
  2. A is invertible.
  3. T is injective.
  4. T is surjective.

Proof

Linear transformations of arbitrary vector spaces


Let V and W be arbitrary vector spaces. A map T from V to W is called a linear transformation if

  1. For every two vectors A and B in V

    T(A+B)=T(A)+T(B);

  2. For every vector A in V and every number k

    T(kA)=kT(A).

In the particular case when V=W, T is called a linear operator in V.

We have seen (see the characterization of linear transformations from Rm to Rn) that linear transformations from Rm to Rn are precisely the maps which satisfy these conditions. Therefore in the case of vector spaces of n-vectors this definition is equivalent to the original definition. Other vector spaces give us more examples of natural linear transformations.

Positive examples.1. Let V be the set of all polynomials in one variable. We shall see later that V is a vector space with the natural addition and scalar multiplication (it is not difficult to show it directly). The map which takes each polynomial to its derivative is a linear operator in V as easily follows from the properties of derivative:

(p(x)+q(x))' = p'(x) +q'(x),
(kp(x))'=kp'(x).

2. Let C[0,1] be the vector space of all continuous functions on the interval [0,1]. Then the map which takes every function S(x) from C[0,1] to the function h(x) which is equal to the integral from 0 to x of S(t) is a linear operator in C[0,1] as follows from the properties of integrals.

int(T(t)+S(t)) dt = int T(t)dt + int S(t)dt
int kS(t) dt = k int S(t) dt.

3. The map from C[0,1] to R which takes every function S(x) to the number S(1/3) is a linear transformation (1/3 can be replaced by any number between 0 and 1):

(T+S)(1/3)=T(1/3)+S(1/3),
(kS)(1/3)=k(S(1/3)).

4. The map from the vector space of all complex numbers C to itself which takes every complex number a+bi to its imaginary part bi is a linear operator (check!).

5. The map from the vector space of all n by n matrices (n is fixed) to R which takes every matrix A to its (1,1)-entry A(1,1) is a linear transformation (check!).

6. The map from the vector space of all n by n matrices to R which takes every matrix A to its trace trace(A) is a linear transformation (check!).

7. The map from an arbitrary vector space V to an arbitrary vector space W which takes every vector v from V to 0 is a linear transformation (check!). This transformation is called the null transformation

8. The map from an arbitrary vector space V to V which takes every vector to itself (the identity map) is a linear operator (check!). It is called the identity operator, denoted I.

Negative examples. 1. The map T from which takes every function S(x) from C[0,1] to the function S(x)+1 is not a linear transformation because if we take k=0, S(x)=x then the image of kT(x) (=0) is the constant function 1 and k times the image of T(x) is the constant function 0. So the second property of linear transformations does not hold.

2. The map T from the vector space of complex numbers C to R which takes every complex number a+bi to its norm sqrt(a2+b2) is not a linear transformation because if we take A=3 and B=4i then T(A+B)=||3+4i||=5 and T(A)+T(B)=3+4=7, so T(A+B) is not equal to T(A)+T(B), so the first property of linear transformations does not hold.

The following theorem contains some important properties of linear transformations (compare with the corollary from the characterization T linear transformations from Rm to Rn and the theorem about products, sums and scalar multiples of linear transformations).

Theorem. 1. If T is a linear transformation from V to W then T(0)=0.

2. If T is a linear transformation from V to W and S is a linear transformation from W to Y (V, W, Y are vector spaces) then the product (composition) ST is a linear transformation from V to Y.

3. If T and S are linear transformations from V to W (V and W are vector spaces) then the sum T+S which takes every vector A in V to the sum T(A)+S(A) in W is again a linear transformation from V to W.

4. If T is a linear transformation from V to W and k is a scalar then the map kT which takes every vector A in V to k times T(A) is again a linear transformation from V to W.

The proof is left as an exercise.

Some properties of linear transformations, which hold for linear transformations from Rm to Rn, do not hold for arbitrary vector spaces.

For example let P be the vector space of all polynomials. Let T be the linear operator which takes every polynomial to its derivative. Then T is surjective because every polynomial is a derivative of some other polynomial (anti-derivatives of a polynomial are polynomials). But T is not injective because the images of x2 and x2+1 are the same (2x). Recall that for linear transformations from Rm to Rn injectiveness and surjectiveness are equivalent.

Notice that since the operator T is not injective, it cannot have an inverse. But let S be the operator on the same space which takes every polynomial to its anti-derivative int(p(t), t=0..x). Then for every polynomial p we have: TS(p)=p (the derivative of the anti-derivative of a function is the function itself). Thus TS=I. On the other hand ST is not equal to I, for, say if p=x+1 then T(p)=1, ST(p)=x, so ST(p) is not equal to p.

For linear operators in Rm, this cannot happen. Indeed, if TS=I then the product of standard matrices of T and S is I. So the standard matrix A of T is invertible, and the standard matrix B of S is the inverse of A. Hence S is the inverse of T and ST=I.

The proof in the last paragraph does not have references to the results that we used. Find these references!

Continue