Potential versus Completed Infinity:
its history and controversy
an essay by Eric Schechter
(version of 5 Dec 2009)
I am not a leading researcher on infinite sets, but I nevertheless attract
a fair amount of email on the subject; I imagine this is mostly because
I have posted several web pages on related subjects. Much of the
email consists of arguments against the notion of a completed infinity.
On this web page I will try to clarify that subject, so that I
don't have to spend so much time answering email. (The
first version of this web page was written on May 7, 2005;
the page probably will evolve over the next few months as I
respond to comments.)
- Potential infinity refers to a procedure that gets closer and closer to,
but never quite reaches, an infinite end. For instance, the sequence
of numbers
gets higher and higher, but it has no end; it never gets to infinity.
Infinity is just an indication of a direction -- it's "somewhere off
in the distance." Chasing this kind of infinity is like chasing a
rainbow or trying to sail to the edge of the world -- you may think
you see it in the distance, but when you get to where you thought
it was, you see it is still further away. Geometrically, imagine
an infinitely long straight line; then "infinity" is off at the "end" of
the line. Analogous procedures are given by limits
In calculus, whether they use infinity or not. For
example, limx to 0 (sin x)/x = 1.
This means that when we choose values of x that are closer and
closer to zero, but never quite equal to zero,
then (sin x)/x gets
closer and closer to one.
- Completed infinity, or actual infinity, is an infinity that one
actually reaches; the process is already done. For instance, let's put braces
around that sequence mentioned earlier:
With this notation, we are indicating the set of all positive integers.
This is just one object, a set. But that set has
infinitely many members. By that I don't mean that it has a large finite number
of members and it keeps getting more members. Rather, I mean that it
already has infinitely many members.
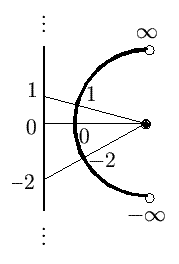
We can also indicate the completed infinity geometrically.
For instance, the diagram
at right shows a one-to-one correspondence between points on an infinitely
long line and points on a semicircle. There are no points for plus or minus
infinity on the line, but it is natural to attach those "numbers" to the endpoints
of the semicircle.
Isn't that "cheating," to simply add numbers in this fashion?
Not really; it just depends on what we want to use those numbers for.
For instance, f(x)=1/(1+x2) is a continuous
function defined for all real numbers x, and it also tends to a limit of 0 when x "goes to"
plus or minus infinity (in the sense of potential infinity, described earlier). Consequently,
if we add those two "numbers" to the real line, to get the so-called
"extended real line," and we equip that set with the same topology as that
of the closed semicircle (i.e., the semicircle including the endpoints), then
the function f is continuous everywhere on the extended real line.
This has some advantages in advanced mathematics:
The topology of the closed semicircle is compact and metrizable.
Compact metric spaces have very nice topological properties; for
instance, every sequence has a convergent subsequence.
Even if we're really just interested in the properties of the
ordinary (finite) real numbers, we can discover
and prove some of those properties more easily by viewing that
set of numbers as a subset of this larger, compact metric space.
History and controversy
Nearly all research-level mathematicians today
(I would guess 99.99% of them)
take for granted both "potential" and "completed" infinity, and most
probably do not even know the distinction indicated by those two terms.
Some of these mathematicians
may be impatient with the few students who still have difficulty
with completed infinities. But their impatience is not justified;
they are forgetting what difficulty the mathematical community
had in reaching its present perspective.
Completed infinity has only been part of mainstream
mathematics since the work of Georg Cantor (1845-1918),
and his ideas initially were met with resistance, because they were not supported
by what we see in the physical world around us.
Before Cantor's time, mathematicians
had struggled with the notion of infinity for many centuries,
mostly without success. Indeed, the fact that the ancient Greeks turned
to geometry rather than algebra can be attributed in part to the
difficulty they had with infinite processes. For instance, the square
root of two can be constructed geometrically in just a few steps,
but to define it algebraically takes some understanding
of an infinite procedure.
Infinity cannot be experienced in our everyday lives, but infinity might be a
good "approximation" to some of the quantities that we read about in the news.
There are 7 billion people in the world, and the annual national budget is
several trillion dollars, and the national debt is many trillions of dollars; all of these
numbers are much bigger than most of us -- even mathematicians --
have any real feeling about. And the number of atoms in the earth is much much
bigger than trillions; I don't even know the name for that number. But still these
numbers are finite.
Nor can we experience the infinitely small in our lives. In fact, the currently
prevailing theories of quantum
physics tell us that there is a lower limit, a smallest physical object.
If we don't see infinity in the physical world around us, then where do
we see it? Why, in our heads, of course. Actually, we see all of
mathematics in our heads. We may see three airplanes or three
apples in the physical world, but the abstract notion of "3" does
not exist in the physical world -- it only exists in our minds.
The notion of "3" is simple enough, and is an abstraction of
enough concrete objects, that there is little chance of our
disagreeing on the notion. Our conversations seem
to suggest that the "3" in my head is very much like the
"3" in your head (though we will never be 100% certain
of that). But more complicated notions
such as infinity, less grounded in physical reality, are
harder to explain; it is harder to be sure that we
are successfully conveying a concept from the
inside of one head to the inside of another.
Cantor's discoveries about infinite sets were just part of a deeper
philosophical revolution
that affected all branches of mathematics,
not just set theory. New
conventions became fashionable, governing what kinds of imaginary
worlds mathematicians would permit inside their heads.
In effect, formalism replaced Platonism.
Many mathematicians today still believe themselves
to be Platonists, and perhaps they can afford that luxury if they work in a small enough
portion of mathematics; but the predominant paradigm of mathematics as a whole
has shifted toward formalism. The birth of mathematical
formalism is most often associated with David Hilbert (1862-1943), but I
think much credit for it is owed to Cantor, and also to a less well
known geometer,
Eugenio Beltrami (1835-1900).
- Probably I am using the word "Platonism" slightly differently from the way that
it is used by philosophers. By mathematical Platonism I mean the view that
mathematics is an attempt to describe some sort of reality, some sort of
absolute truth --- and that there is, in fact, just one correct absolute truth.
Perhaps a better word would be monism, emphasizing that there
is only one truth. This was the predominant view until the late
19th century. For instance, geometry was our best attempt at
describing physical space, and it was certainly Euclidean. Any
non-Euclidean geometry was obviously wrong, a pack of lies,
at best a work of fiction. In fact, before Beltrami's time,
considerable effort was spent in trying (unsuccessfully)
to show that the axioms of any
non-Euclidean geometry must inevitably yield a contradiction.
- By formalism I mean the view that mathematics does not need to
be grounded in physical reality. We can start from whatever axioms we
like (though we are urged to at least exercise some good taste in
choosing our axioms). We then investigate what consequences can
be proved from our axioms. Perhaps a better term for this viewpoint
would be pluralism, referring to the fact that there can be
many truths. For instance, the sum of the three angles of a triangle
add up to exactly two right angles if you're working on a
Euclidean plane, or more than two right angles if you're working
on the surface of a sphere, or less than two right angles if
you're working on a saddle surface. (In the last two cases,
you don't have straight lines, so
you have to redefine "triangle." For the side of a triangle,
use the shortest path between two vertices of the triangle.)
Beltrami's 1868 paper showed that
certain non-Euclidean systems of axioms
are modeled (i.e., satisfied)
within Euclidean geometry
by spheres, saddles, etc.
From this mathematicians
saw that the non-Euclidean axioms cannot
lead to a contradiction (unless Euclidean geometry
itself is contradictory).
Formalism and its consequences were controversial at first.
One of the more visible battle lines was between
the group now known as classicists (who believe that
mathematics is a collection of statements) and
constructivists (who believe that mathematics is a
collection of constructions or procedures).
The overwhelming majority of mathematicians today are
classicists, but this is merely a matter of personal
preference (like one's favorite color), not a matter
of someone being right or wrong. Nearly
any mathematician
today who understands both sides of the issue agrees
that both sides make perfectly good sense. (On the
other hand, many classicists today are entirely
unfamiliar with the constructivist viewpoint.)
A striking example is
the Axiom of Choice (described in greater
detail on
another
web page). This axiom,
acceptable to classicists
but not to constructivists,
is a nonconstructive assertion of the "existence"
of certain
sets or functions.
The use of the word "exist"
is merely a grammatical convenience here;
mathematicians and nonmathematicians do not
mean quite the same thing by this word.
Unfortunately, we mathematicians
don't have a better word; to
be more precise we would have to replace this
one word with entire paragraphs.
If we assume the
Axiom of Choice, we are not really stating that we
believe in the physical
"existence" of those sets or functions.
Rather, we are stating that (at least for the moment)
we will agree to the convention that we are permitted
write proofs in a style
as though those sets or functions exist.
Whether those sets or functions "really" exist is
actually not important, so long as they do not give
rise to contradictions. Mathematicians are perfectly
willing to use devices that may be fictional,
as intermediate
steps in getting from a real problem to a real solution.
Perhaps the most striking example of this is
the use of so-called "imaginary numbers" such as i,
the square root of -1 (described in
greater detail on another web page).
Such numbers were first
developed for the purpose of
solving certain polynomial equations. Initially,
the attitude mathematicians took was, "there cannot
really be a square root of -1, but if such
a number did exist, what would its properties be?"
Many decades later, it was discovered that those
properties correspond, in a natural way, to
the process of rotating
the Euclidean plane through a quarter turn.
The number i is very useful to engineers,
for solving differential
equations involving sines, cosines, and other functions
related to rotation. That's very real, not at all fictitious.
Nevertheless, the name "imaginary" stuck.
The formalist revolution
took longer to reach some branches of
mathematics
than others. One of the late arrivals was mathematical logic.
One type of logic, now known as "classical logic," was
given almost exclusive sovereignty until perhaps as late
as 1960, and only gradually began to share its power
with nonclassical logics during the last decades of the
20th century. Perhaps this delay was caused by
the fact that, around 1930, Kurt Gödel made some
highly interesting and important contributions to
classical logic, thereby distracting people away from
other logics. Classical logic is adequate
for the needs of most mathematicians, and it
is computationally the simplest of the main logics,
but it disregards qualities such as
constructiveness, relevance, and causality.
The study of those qualities has led to alternative
logics, some of which are discussed further
on the web page advertising my
logic book.
Though the formalist revolution is an undeniable fact of mathematical
(and perhaps scientific) history, some questions about it still remain --
e.g., is formalism good or bad? Some scientists and
mathematicians have suggested that mathematics, no
longer tied to its origins in physics, is developing into a
baroque art form, a thing of great embellishments and
few uses; that mathematics has been reduced
to a mere game of meaningless marks on paper.
Others have argued that mathematics
turns out to be useful in surprising and unexpected
ways, just because mathematicians have concerned
themselves with the investigation of the fundamental
properties of basic mathematical objects, such
as numbers.
Perhaps the most famous essay on this subject
is
The
Unreasonable Effectiveness of Mathematics in the Natural Sciences,
published in 1960 by Eugene Wigner.
