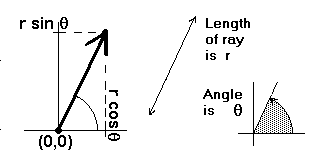| It is true that
the real numbers are 'points on a line,' but that's not the whole
truth. This web page explains that the real number system is a
Dedekind-complete ordered field. The various concepts are
illustrated with several other fields as well. Version of
11 Nov 2009 by Eric
Schechter. If you find any errors, or see anything that
isn't explained clearly enough, or have any other comments about
this page, please write to
me. |
What are the "real numbers,"
really?
The short, simple answer used in
calculus courses is that a real number is a point on
the number line. That's not the whole truth, but it
is adequate for the needs of freshman calculus.
The freshman calculus course (at most universities
nowadays) follows the 17th century style of Newton
and Leibniz, emphasizing computations and omitting many
proofs. The omitted proofs depend on
a careful explanation of what the "real numbers"
really are.
That explanation and those proofs were not discovered
until the 19th century, after Newton and Leibniz were
long dead.
A proper explanation of the real numbers nowadays
is covered, if at all, in a course in "real analysis"
in the junior or senior year of students who are majoring
in mathematics. Surprisingly few students take such a
course; perhaps that's because it is too algebraic for the
analysts' taste and too analytic to please the algebraists.
In this web page, I'll discuss the mathematical meaning
of "real number." Before that, I want to discuss this
more elementary question: where did the name "real" come
from? (It turns out to have little to do with the deeper
properties of real numbers.) To answer that question, I
first need to talk about complex numbers.
Treating points in the plane as numbers
There is a natural way to "add" or "multiply" two
points in the Euclidean plane. By "natural" I mean
that the definitions have turned out to be useful for
many applications, and that the definitions are fairly
simple. Unfortunately, the definitions take their simplest
forms if we use different coordinate systems for the
addition and multiplication operations.
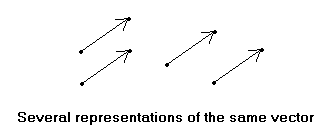
- The
"addition" of points is described most simply
as vector addition. A
vector can be represented by a directed line-segment;
two vectors are considered equal if they
point in the same direction and have the same
length. (See diagram.) We can change the representation of a vector
by moving it (i.e., "translating" it) to a new position
parallel to the original position.
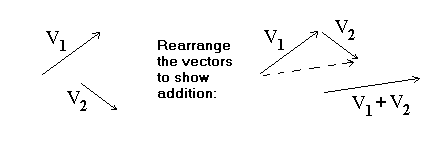 To add two vectors V1 and V2,
represent them with directed line-segments so that
the initial end of V2 is located
at the terminal end of V1. Thus
the arrows in the diagram form a path: start at
the initial end of V1, proceed to its
terminal end, then turn a corner and follow
V2 from its initial end to its
terminal end. The sum, or resultant,
V1+V2,
is the journey going from the initial end
of V1 to the terminal end of
V2. That sum is represented by a single
directed line-segment, the dashed third side of the
triangle.
To add two vectors V1 and V2,
represent them with directed line-segments so that
the initial end of V2 is located
at the terminal end of V1. Thus
the arrows in the diagram form a path: start at
the initial end of V1, proceed to its
terminal end, then turn a corner and follow
V2 from its initial end to its
terminal end. The sum, or resultant,
V1+V2,
is the journey going from the initial end
of V1 to the terminal end of
V2. That sum is represented by a single
directed line-segment, the dashed third side of the
triangle.
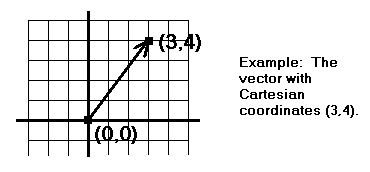 To
represent vectors with the Cartesian coordinate system,
draw a vector V so that its initial end is at the
origin (0,0). Then the coordinates of the location of
its terminal end are used as the coordinates of the
vector. (See diagram.)
To
represent vectors with the Cartesian coordinate system,
draw a vector V so that its initial end is at the
origin (0,0). Then the coordinates of the location of
its terminal end are used as the coordinates of the
vector. (See diagram.)
If we use that coordinate
system, then the formula for vector addition is very
simple: The first coordinate of
V1+V2 is the sum of the first
coordinates of V1 and V2, and the
second coordinate of V1+V2 is
the sum of the second coordinates of V1 and
V2. That is,
| (a,b) +
(c,d) = (a+c, b+d) |
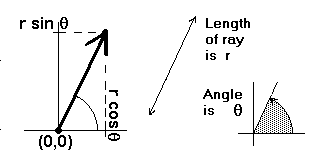
- The
"multiplication" that we want to use can also be described in
Cartesian coordinates: (a,b) ⋅
(c,d) = (ac−bd, ad+bc). But that's a
bit complicated and nonintuitive; it looks somewhat arbitrary and
contrived. We get a much simpler, more geometrically appealing
definition if we switch to polar coordinates. Let a point be
represented by <r,θ> if it has
radius r and angle θ -- i.e., if it is
located r units away from the origin, and on a ray that is θ
radians counterclockwise from the ray that
points toward the right. That point has Cartesian coordinates
(r cosθ, r sinθ). If you substitute those values into
our Cartesian formula for multiplication, and then simplify
using some trigonometric identities, you'll end up with this
much simpler definition of multiplication:
If
P1 has polar coordinates <r1,θ1> and P2 has polar
coordinates <r2,θ2>, then
the product
P1P2 is defined to be the point with polar
coordinates <r1r2, θ1+θ2>. |
In other words, multiply the radii and add the angles. The
effect of multiplying points in the plane by P2 is to
rotate the plane through an angle of θ2 and stretch (or shrink)
the plane by a magnification factor of r2. This
concept is very simple, and it's quite useful in engineering,
which is often concerned with describing rotations (e.g., of
engines).
When addition and multiplication are defined as above, then
the points in the plane are called complex numbers,
for reasons that will be discussed a few paragraphs from
now.
Since (a,0)+(c,0)=(a+c,0) and (a,0)×(c,0)=(ac,0), the points along the
horizontal axis have an arithmetic just like "ordinary" numbers;
we will write (a,0) more briefly as a. For instance, (5,0)
will be written as 5. The points along the
vertical axis also have a shorter notation: the point (0,b) will
be written more briefly as bi; for instance, (0,5) will
be written as 5i. The i stands for "imaginary", for
reasons explained below.
Important exercises.
Using either the formula
(a,b) ×
(c,d) = (ac−bd, ad+bc) or
the definition in terms of polar coordinates, the beginner should
now verify that
i2 = −1.
That will be important in the discussion below.
Here are the answers to those two exercises:
Using the Cartesian coordinate system, we compute
i2 = (0,1)
× (0,1)
= (0•0−1•1, 0•1+1•0)
= (−1,0) = −1. Or, using polar coordinates: The number i has
radius 1 and angle π/2.
Hence the number
i2 has radius
1•1=1 and angle
(π/2) + (π/2)
= π;
the complex number with those polar coordinates is −1.
What's "real" about the real numbers?
Probably the simplest way to understand "complex numbers" is to
start with points in the plane, as I have done in the
preceding paragraphs. However, by a
historical accident, the simplest explanation was not the first
explanation discovered. Indeed, the geometric,
points-in-the-plane viewpoint wasn't discovered until the 19th
century, long after the algebraic computations had been
investigated. As early as the 16th century, mathematicians were
devising new "numbers" as a way of solving polynomial equations;
they were thinking in terms of algebraic formulas rather than pictures.
They were particularly interested in the third and fourth degree
equations at that time, but they even had new insights into the
quadratic equation.
The attitude that they took was something like this:
|
We all know that there isn't really any "number" p
that can satisfy the equation
p2 = −1. Such
a "number" can only exist in our imagination. But if it
somehow did exist, what kind of arithmetic rules
would it have to follow?
|
You have to admire
the genius of the 16th century mathematicians: They
correctly worked out the arithmetic rules of the complex
numbers despite their lack of the simple geometric model;
they calculated with "numbers" whose existence they didn't
even believe in!
Their terminology was unfortunate, however.
There is nothing fictitious or dreamlike
about rotations of engines, but the name
stuck. The points on the vertical axis
are now called imaginary numbers, despite the fact
that they have very tangible applications.
The points on the horizontal axis are
(by contrast) called real numbers.
All the points in the plane are called
complex numbers, because they
are more complicated -- they have both
a real part and an imaginary part.
Thus ends our tale about where the name "real number"
comes from. But we have barely begun investigating the
mathematical properties associated with that name.
Getting rid of the pictures
The "point on a line" answer is not a fully satisfactory
answer, because it is not
axiomatic or algebraic. It relies on pictures that we don't
really understand. For instance,
the set of real numbers and the set of rational numbers
have essentially the same picture,
but their algebraic properties differ in ways
that are very important for analysts.
Imagine studying that picture of a line under a super microscope.
If you could magnify the line at a very high power -- say at a
magnification of a googolplex, or better yet a magnification of
infinity -- would it still look the same? Or would you see a row
of dots separated by spaces, like the dots in a picture in a
newspaper? (It turns out that, in some sense, the real numbers
would still look like a line under infinite magnification, but the
rational numbers would be dots separated by spaces. But that is
only a vague and intuitive statement, not anything precise that
we can use in proofs.)
The only way to get rigorous answers to these questions is to
set up a very careful system of axioms about geometry ... but
that amounts to the same thing as setting up a careful set of
axioms about the algebraic properties of the real numbers. It
turns out that the latter is a little easier, so we may as well
concentrate on the algebraic aspects of the situation. To answer
questions like this, ultimately we have to get away from the
pictures; we have to understand the real numbers entirely in
terms of formulas.
As a preview, here is the definition that we're going to end up with:
the real line is a Dedekind-complete
ordered field. That's complicated, so we'll work our
way up to it in stages. We'll discuss:
- What is a field?
- What is an ordered field?
- What is a Dedekind-complete ordered field?
- Why do I say that the real line is a
Dedekind-complete ordered field? How can that be a definition?
Groups and fields
First of all, a group is a mathematical object;
it is a triple (X,e,*) with these properties:
- X is a nonempty set.
- e is a specially chosen member of the set X. It is called the
identity of the group.
- * is a binary operation on X, which we may call the
group operation. This means that whenever p and q are
members of X, then p*q is also a member of X.
- (p*q)*r = p*(q*r)
for all p,q,r in X.
- p*e = e*p = p for every p in X.
- For each p in X, there exists at least one corresponding
q in X that satisfies p*q = q*p = e. (It can be shown that there is
at most one such q, and thus q is uniquely
determined by p; we call q the inverse of p.)
Exercises:
- The identity is uniquely
determined
--- i.e., if
p*e1 = e1*p = p
and
p*e2 = e2*p = p
for all p in X, then
e1 = e2.
- Inverses are uniquely determined --- i.e., if
p*q1 = e and
p*q2 = e then
q1 = q2,
The group is said to be abelian (or commutative) if it also satisfies this property:
- p*q = q*p for all p,q in X.
Examples:
- (Z,0,+) is an abelian group, where Z is the set of
all integers
- ({even integers}, 0,+) is an abelian group
- ({-1,1}, 1, x) is an abelian group
- (R+,1,x) is an abelian group, where R+ is the set of
all positive real numbers
- (R\{0},1,x) is an abelian group, where R\{0} is the
set of all
nonzero real numbers. (Here "\" means the difference of two sets.)
- (T,1,x) is an abelian group, where T is the set of
all
complex numbers that lie along the unit circle centered
at 0
Now, a field is a quintuple (Y,0,+,1,×) with these properties:
- Y is a set, 0 and 1 are two specially chosen members of Y, and + and
× are two
binary operations on Y.
- 0≠1.
- The triple (Y,0,+) is an abelian group.
- The triple (Y\{0},1,×) is an abelian group.
(Note that this group has for its
set of members, all the members of Y except 0.)
- p×(q+r) = (p×q) +
(p×r) for all p,q,r in Y.
(Exercise: A few mathematicians do not include the
requirement
that 0≠1. Prove that there is only
one "field" in which 0=1. For that field, the set Y has
only one member.)
Here are a few examples:
- The rational numbers (i.e., numbers like 3/4 and -171/25) are a field.
- The real numbers (i.e., numbers like 87.324116279...) are a field.
- The complex numbers are a field. (Exercise: Verify all the
axioms. Also, what is the multiplicative inverse of 3+2i ?)
- The set of all
numbers of the form p+q√2, where
p and q are rational numbers, is a field; it is a subset of
the
reals and a superset of the rationals. (Exercise:
Verify all the axioms. Also, what is the multiplicative
inverse of
3+2√2 ?)
Following is one more example. We will present a
finite field -- that is, a field with only finitely many members. For the
set Y, we'll use Y={0,1,2,3,4}. For its addition and multiplication operations,
we'll use ordinary addition and multiplication, modified by this rule:
If the result of addition or multiplication results in a number greater than 4,
subtract 5 or 10 or 15, to get a number in the set Y again.
In other words, we'll use these tables for addition and multiplication:
| + |
. |
0 | 1 | 2 |
3 | 4 |
| . |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
|
| × |
. |
0 | 1 | 2 |
3 | 4 |
| . |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
|
This field is sometimes called arithmetic modulo 5.
(Exercises: Show that a similar field can be given
with 5 replaced by any prime number. Show that there is
also a field with 4 elements, and a field with 9 elements,
but there is no field with exactly 6 elements. Much much
harder: It can be shown that there is a field with exactly
n elements, for some integer n, if and only if n is of the
form pr for some prime number p.)
Ordered fields
Next, we need to define an ordered field. This is a sextuple
(Y,0,+,1,×,<) where
The reals and the rationals, with their usual
orderings are two familiar examples of ordered fields.
A slightly less familiar example is given by the set of all
numbers of the form p+q√2, where
p and q are rational numbers. (Exercise: Show that that set is an
ordered field.)
It can be shown that every ordered field contains, as a subset, an
isomorphic copy of the rational numbers -- i.e., a set that is
identical to the rational numbers in all its arithmetic operations;
it may differ only in the names of some things, via a change in labeling.
If you relabel things a bit, you can say that the
rational numbers are a subset of every ordered field.
In particular, every ordered field contains infinitely many
members.
Therefore,
the field of the arithmetic modulo 5 cannot be made into an ordered field
by defining < in some clever way.
It can also be proved that, in any ordered field
- −1 < 0, and
- if
p ≠ 0, then
p2 > 0.
Since i2 = −1,
it follows that there is no way that we can make the
complex numbers into an ordered field, no matter how we
define
<.
Infinitesimals
This next part is optional -- i.e., you can get through the definition
of the real numbers without ever thinking about infinitesimals. But I think
this next part is interesting, and also makes the definition
of the real numbers easier to understand.
About 300 years ago, Newton and Leibniz invented calculus.
Well, that's an oversimplification. Some of the ideas of
calculus were already around, but they cleaned it up and
knitted it together with what we now call the Fundamental
Theorem of Calculus. Newton also showed some of the ways
calculus can be used -- he worked out many of the basic laws
of physics, and showed how to compute the orbits of the
planets much more simply and accurately than anyone had ever
done before. In doing so, he contributed greatly to the
beginning of the Age of Enlightenment -- an age in which
people realized that they can accomplish quite a lot through
reasoning, and that they don't have to just live in fear,
superstition, and confusion. This may have indirectly
contributed to things like the industrial revolution and
the birth of democracy.
Anyway, Newton and Leibniz knew how to do many of the
computations
that we now teach in calculus, but they didn't know how
to do satisfactory proofs of the theory behind
calculus. They tried to do proofs, but their explanations
were a bit lacking. Many of their explanations were
based on infinitesimals -- i.e., numbers that
are infinitely small but not zero. For instance, in
their explanations, dy/dx did not represent a limit
of changing numbers. It represented a quotient of
unchanging numbers, but those numbers were
infinitesimals.
The computations of Newton and Leibniz were accepted by
other mathematicians, but the proofs were not. The
explanation of infinitesimals didn't entirely make sense,
and mathematicians were uncomfortable with it.
In the following centuries, Cauchy and Weierstrass
produced the epsilon-delta proofs that we now find
in calculus textbooks. Those proofs involve numbers
that are of "ordinary" size (not infinitesimal), but
the numbers would vary through many different ordinary
sizes;
thus we take the limit as epsilon changes toward zero.
In our textbooks, dy/dx represents the limit of a changing
quotient of two ordinary numbers.
In the late 19th century, Dedekind finally gave a
clear explanation of the real numbers (which we'll
sketch at the end of this web page), and we can
prove that in Dedekind's
number system there are no infinitesimals.
Arguments with infinitesimals
were no longer needed and fell out of favor.
Ultimately, infinitesimals were discredited and discarded
by mathematicians (though they
continued to be mentioned in some physics books
many decades later).
In the 1960's, mathematician
Abraham Robinson finally figured out
how to make sense out of infinitesimals. Thus
nonstandard analysis was born. It involved some
nonstandard real numbers, among which we can
find some infinitesimals. In the paragraphs below, I will
give an example of an ordered field that has some
infinitesimals. The discussion below is based on
20th-century ideas, not just on those of Newton and Leibniz.
I should mention, however, that the example that I will
present is not the approach preferred by the
nonstandard analysts. They prefer an approach that is more
complicated but also more powerful. (It involves making
careful logical analysis of a formal first-order language,
but we don't need to discuss that here.)
Some of the nonstandard analysts now actually feel that
infinitesimals yield a better understanding of calculus.
After all, it gave Newton and Leibniz the intuition that
they needed. We can actually make rigorous mathematics,
with only slight adjustments in the ideas of Newton
and Leibniz. (For instance, the derivative should be
the standard part of that quotient of infinitesimals;
this term is explained in a later paragraph below.)
But most mathematicians still prefer the
epsilon-delta approach, which they feel is simpler. (Both
methods are correct, and both yield the same results.) At
any rate, some discussion of infinitesimals may be helpful
in our explanation of ordered fields.
|
Definitions.
Suppose that Y is an ordered field. An infinitesimal
member of Y is a member r, other than 0, that satisfies all
of these infinitely many conditions:
−1 < r < 1 ,
−1/2 < r < 1/2 ,
−1/3 < r < 1/3 ,
...
Two members of Y are said to be infinitely close if
their difference is an infinitesimal.
|
Some ordered fields have infinitesimals, and some don't.
The ordered fields that have no infinitesimals are called
Archimedean fields; we'll see later that the real
number system (i.e., Dedekind's number system,
also known as the standard real numbers)
is Archimedean. The ordered fields that do have
infinitesimals are called non-Archimedean fields;
we'll give an example of such a field in the next
few paragraphs.
The example will be based partly on rational functions.
By a rational function in the variable t, we will
mean a function of the form p(t)/q(t), where p(t) and q(t)
are polynomials with standard real coefficients, and q is
not the constant polynomial 0. Note that each real number
can be viewed as a rational function -- for instance, the
number 7 can be viewed as 7/1, where 7 and 1 are both
polynomials of degree 0. Thus the set of real numbers is a
subset of the set of rational functions.
(Of course, to make sense of this, we have to assume
that we already have some understanding of the real numbers.
But we won't need a very deep understanding; the
"points on a line" conception will suffice for now.)
We define addition and multiplication of rational functions
in the usual fashion, as in high school algebra. However, we make this
one alteration in the usual treatment of rational functions: We will
consider two rational functions to be "the same" if they agree except at
finitely many values of t. For instance, these two functions
are not really the same, because the first one is defined at
t = −2 and the second one is
not. But the
two functions are identical for all other values of t, so we will
view them as "the same" for purposes of the present discussion.
With that convention, it can be shown that the set of all
rational functions is a field.
Also, the real numbers are a subset of the rational
functions. For instance, the constant 1 and the constant 7
are polynomials of degree 0, so the constant 7/1 is a
rational function. In this fashion we can view every
real number as a rational function.
We can make the rational functions into
an ordered field, if we just
define the right ordering. To do so, we will make use of the
following theorem. (We will omit the proof of the theorem,
which is a bit harder, but it just involves some advanced
calculus and some college algebra.)
Theorem.
Suppose that q(t) and r(t) are given rational
functions in the variable t. Then there exists some real number
t0 (which may depend on the choice of q
and r) such that exactly one of these three cases
holds:
- For every real number t > t0, the real number
q(t)
is less than the real number r(t).
- For every real number t > t0, the real number
q(t) is equal to the real number
r(t).
- For every real number t > t0, the real number
q(t) is greater than the real number
r(t).
Furthermore, if case 2 holds, then q(t) =
r(t) for all but finitely many values of
t. |
We now define an ordering on the rational functions, by saying
that
q < r or
q = r or
q > r
if cases 1, 2, or 3 hold, respectively. In other words, one rational
function is less than another if it is eventually less -- i.e., if
it is less when we go far enough to the right on the graphs of
the two functions. How far to the right we have to go may depend
on which two functions we're looking at; but the theorem says that
for each choice of two rational functions, there is some point
after which one function stays below the other (unless they're the
"same").
With this definition of ordering, it turns out
that the set of rational functions is an ordered field. But it also
turns out that the functions
1/t, 2/t,
1/t2,
etc.,
are infinitesimals. Thus, the field of rational
functions is non-Archimedean, when ordered as we have described.
How does this relate to Newton's view of numbers?
I'm sure that Newton wasn't thinking of his infinitesimals
as rational functions. But we can get some idea of his
viewpoint,
as follows:
There are no infinitesimals among the standard real numbers.
But we could imagine that, with a sufficiently powerful
microscope, we might discover some additional "nonstandard"
numbers that we had not noticed before. Nestled around each
standard real number r, infinitely close to it, are infinitely
many new nonstandard numbers. (Then r is the standard part of any
of those new numbers.) In particular, nestled around
0 are the infinitesimals. We can also get some other
nonstandard numbers by taking the reciprocals of the
infinitesimals; those numbers are infinitely large. The
collection of all the numbers -- both "standard" and "new",
together -- is an ordered field. Its ordering is the same
as the ordering of the set of rational functions.
Least upper bounds
Suppose that Y is an ordered field, and S is a nonempty subset of Y, and
b is a member of Y. We say that b is an upper bound for the set S
if we have s < b satisfied for every s in S.
If the set S has an upper bound, then in general it has many upper bounds.
Say B is the set of upper bounds of S, and B is nonempty. Does B have
a lowest member? If it does, that member is called the least upper bound
of the set S.
The word "complete" has different meanings in different branches
of mathematics. Generally, an object is called "complete" if
there are no "holes" in it -- i.e., if nothing that seemingly
"ought to" be there is missing. This vague description
has different meanings for different kinds of mathematical
objects -- a complete ordered field, a complete measure space,
a complete logic, etc. Here, we will only
consider the meaning of completeness
for ordered fields.
An ordered field Y is said to be complete, or Dedekind complete,
if it has this property, also known as the
least upper bound property:
|
Whenever S is a nonempty subset of Y, and S has at least one upper bound,
then S has a least upper bound.
|
Dedekind completeness turns out to be crucial in analysis,
because it enables us to take limits.
Some ordered fields are Dedekind complete, and some aren't. Here
are two quick examples of ordered fields that aren't complete:
- The set of rational numbers is incomplete
(i.e., not complete).
To see this, let S be the set of all rational numbers r that satisfy r2 < 5.
Then S has many upper bounds -- for instance, 3 is an upper bound, and 2.24
is another upper bound, and 2.23607 is another
upper bound. We can keep finding more of these numbers -- whatever rational
number we propose for an upper bound for S, it is possible to find another
rational number that is still a little lower and that is also an upper bound
for S. You can probably see why already: These numbers are converging to
√5 = 2.23606797749978969640917366873128...
But that number is not rational. Any rational upper bound for S would have
to be slightly higher than √5, and between that
rational number and √5 we can always find still another
rational number. In the field of rational numbers, the set S does not have a
least upper bound.
- If Y is a non-Archimedean field -- i.e.,
an ordered field that has infinitesimals -- then Y
is incomplete. One way to see this is
to let S be the set of all infinitesimals. Since some of the
infinitesimals are positive, any upper bound for S must be
greater than 0. Note that 1 is an upper bound for S, and 1/2 is
another upper bound for S, and 1/3 is another upper bound for S,
and so on. Suppose (for contradiction) that
b were the least upper bound for S.
Then b must be positive, and must be less than or equal to all of
the numbers 1, 1/2, 1/3, etc. -- thus b must be a positive
infinitesimal. Then 2b is also an infinitesimal, so 2b is a
member of S. Since b is an upper bound for S, that tells us
2b < b. But b < 2b since b is
positive. This is a contradiction.
(Note that, conversely, any complete ordered field must
be Archimedean.)
Complete fields
We have used the real numbers in some of our preceding
discussions. For instance, the complex numbers are ordered
pairs of real numbers, and our example of infinitesimals
involved rational functions with real coefficients. In
effect, we "borrowed" the real numbers -- we used the reals
in examples, even though we hadn't formally defined them
yet; we just relied on the informal and intuitive
understanding that students already have, based on the
geometric line. Trust me, there is no circular reasoning
here -- I won't use the "borrowed" concepts when I finally
get around to defining the real numbers. You'll see that if
you actually work through all the details. (I'm not
claiming that this web page is more than an outline.)
The definition of the reals depends on two more theorems, both
of which are difficult to prove.
|
Theorem 1. There exists a
Dedekind-complete ordered field. |
The literature contains
many different proofs of this theorem.
I think three are simple enough to deserve mention here:
- Proof using decimal expansions.
Let Y be the set of all infinite decimal expansions --
i.e., expressions such as 3.682951... and −17.311897... . Adopt the convention
that 2.719999... is the "same" as 2.7200000..., etc. Use
the usual operations of addition and multiplication. Then Y
is a complete ordered field, but verifying that fact is
extremely tedious. It generally isn't worked out in full
detail. One place that you can find it in fairly complete
detail is in J. F. Ritt, Theory of Functions, 1946.
It is also sketched in
M. Rosenlicht, Introduction to Analysis,
reprinted by Dover.
- Proof using Dedekind cuts.
Let Q be the set of rational numbers; we assume that we already
have a good understanding of those. By a Dedekind cut we mean a pair
(A,B) with these properties:
- A and B are nonempty subsets of Q whose union is Q
- a < b, for every a ∈ A and every
b ∈ B
- A has no highest element.
The set B might or might not have a lowest element.
Here are some examples of cuts in which B has a lowest element:
A-2 = {x ∈ Q: x < -2},
B-2 = {x ∈ Q: x
> -2}
A3.7 = {x ∈ Q: x < 3.7},
B3.7 = {x ∈ Q: x
> 3.7}
and here is an example of a cut in which
B has no lowest element:
A = {r ∈ Q:
r < 0 or
r2 < 5},
B = {r ∈ Q:
r >0 and r2 > 5}.
(That cut would be called
(A√5,
B√5)
if we had a √5.)
The set of all cuts can be made
into a complete ordered field, if we define addition and multiplication
the right way. Again, it's tedious; you can find some of the details
worked out in W. Parzynski and P. Zipse,
Introduction to Mathematical Analysis.
- Proof using Cauchy sequences.
Again start from the rational numbers. Say that a sequence
r1, r2, r3, ...
of rational numbers is a Cauchy sequence if
it has the property that
|
for each positive integer p there exists a positive integer m (which may
depend on p and on the particular sequence being studied) such that,
whenever i and j are greater than m, then
|ri − rj| < 1/p. |
Now, say that two Cauchy sequences
r1, r2, r3, ...
and
s1, s2, s3, ...
of rationals are equivalent if they have the property that
| for
each positive integer p there exists a positive integer m
(which may depend on p and on the particular sequences being
studied) such that, whenever i is greater than m, then
|ri − si| < 1/p. |
By an equivalence class we mean the set of all the sequences that are equivalent
to some particular sequence. Now, it can be shown that the
set of all equivalence classes is a complete ordered field, if we define
addition and multiplication on it in the right fashion.
This proof, due to Cantor, is a slight modification of a proof that
can be found in many analysis or topology books, showing that every
metric space has a metric completion.
The other theorem is harder to prove, and I won't even
sketch a proof here. In fact, this theorem is even
difficult to state:
|
Theorem 2. Any two
Dedekind-complete ordered fields are isomorphic
i.e., there exists a one-to-one correspondence between
them that preserves, in both directions, the orderings
and the arithmetical operations. Thus, any two
Dedekind-complete ordered fields are essentially "the same";
one is simply a relabeled copy of the other. |
In particular, the decimal expansions, the Dedekind cuts, and the
equivalence classes of Cauchy sequences, though they appear to be entirely
different, all turn out to have the same arithmetic and algebraic
structure -- they are really the "same" object. It is that object
which we call the real number system.
Finally, the real definition of the reals
(No pun intended.)
|
Definition. The real number system
is that unique algebraic structure represented by all
Dedekind-complete ordered fields. |
You might wonder why mathematicians want to use such a complicated
definition. Wouldn't it be easier to simply define the real numbers
to be the Dedekind cuts, or define the real numbers to be the
decimal expansions, or something like that? That is the approach
taken in some elementary textbooks, but ultimately it is less
productive. When we actually use the real number system in proofs,
the properties that we need are not specifically the properties of
(for instance) Dedekind cuts or of decimal expansions. Rather, the
properties we need are the axioms of a Dedekind complete ordered field.
It is much simpler to think in terms of those axioms.
To think of "numbers" as being cuts or expansions would
just encumber us with extra baggage.
The cuts or expansions are models -- they are
useful for the job proving Theorem 1, but they are useful for little else.
Once they've done that job, we can discard and forget them.
If you wish, you can now think of the points on a line as
representing the members of a Dedekind-complete
ordered field. It is then correct to say that the real
numbers are the points on a line.

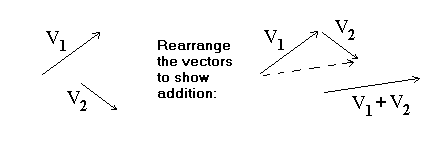 To add two vectors V1 and V2,
represent them with directed line-segments so that
the initial end of V2 is located
at the terminal end of V1. Thus
the arrows in the diagram form a path: start at
the initial end of V1, proceed to its
terminal end, then turn a corner and follow
V2 from its initial end to its
terminal end. The sum, or resultant,
V1+V2,
is the journey going from the initial end
of V1 to the terminal end of
V2. That sum is represented by a single
directed line-segment, the dashed third side of the
triangle.
To add two vectors V1 and V2,
represent them with directed line-segments so that
the initial end of V2 is located
at the terminal end of V1. Thus
the arrows in the diagram form a path: start at
the initial end of V1, proceed to its
terminal end, then turn a corner and follow
V2 from its initial end to its
terminal end. The sum, or resultant,
V1+V2,
is the journey going from the initial end
of V1 to the terminal end of
V2. That sum is represented by a single
directed line-segment, the dashed third side of the
triangle.
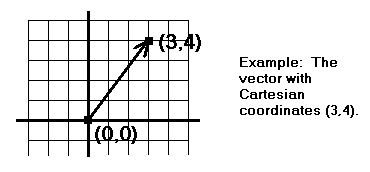 To
represent vectors with the Cartesian coordinate system,
draw a vector V so that its initial end is at the
origin (0,0). Then the coordinates of the location of
its terminal end are used as the coordinates of the
vector. (See diagram.)
To
represent vectors with the Cartesian coordinate system,
draw a vector V so that its initial end is at the
origin (0,0). Then the coordinates of the location of
its terminal end are used as the coordinates of the
vector. (See diagram.)