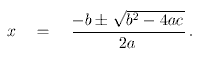
I'm putting this on the web because some students might find it interesting. It could easily be mentioned in many undergraduate math courses, though it doesn't seem to appear in most textbooks used for those courses. None of this material was discovered by me. -- ES
You should know that the solution of ax2+bx+c=0 is
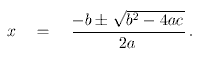
There is an analogous formula for polynomials of degree three: The solution of ax3+bx2+cx+d=0 is
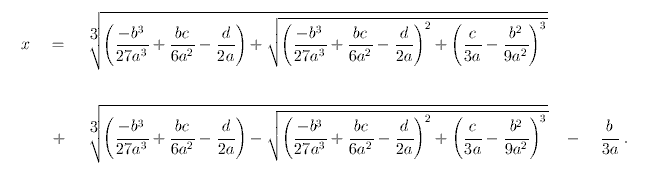
(A formula like this was first published by Cardano in 1545.) Or, more briefly,
where
But I do not recommend that you memorize these formulas.
Aside from the fact that it's too complicated, there are other reasons why we don't teach this formula to calculus students. One reason is that we're trying to avoid teaching them about complex numbers. Complex numbers (i.e., treating points on the plane as numbers) are a more advanced topic, best left for a more advanced course. But then the only numbers we're allowed to use in calculus are real numbers (i.e., the points on the line). That imposes some restrictions on us --- for instance, we can't take the square root of a negative number. Now, Cardan's formula has the drawback that it may bring such square roots into play in intermediate steps of computation, even when those numbers do not appear in the problem or its answer.
For instance, consider the cubic equation x3-15x-4=0. (This example was mentioned by Bombelli in his book in 1572.) That problem has real coefficients, and it has three real roots for its answers. (Hint: One of the roots is a small positive integer; now can you find all three roots?) But if we apply Cardano's formula to this example, we use a=1, b=0, c=-15, d=-4, and we find that we need to take the square root of -109 in the resulting computation. Ultimately, the square roots of negative numbers would cancel out later in the computation, but that computation can't be understood by a calculus student without additional discussion of complex numbers.
There is also an analogous formula for polynomials of degree 4, but it's much worse to write down; I won't even try here.
There is no analogous formula for polynomials of degree
5. I don't just mean that no one has found the formula
yet; I mean that in 1826 Abel proved that there cannot
be such a formula. The problem is that the functions
![]() don't do enough of what you need for
solving all 5th degree equations. (Imagine a calculator
that is missing a few buttons; there are some kinds of
calculations that you can't do on it.) You need at least
one more function. One such function, for instance, is
the inverse of the function f(x)=x5+x. (There are
other functions that would also work, and some of them
are more interesting to mathematicians for various
reasons, but I like this one because it can be described
in fairly elementary terms.) That function, together
with the functions
don't do enough of what you need for
solving all 5th degree equations. (Imagine a calculator
that is missing a few buttons; there are some kinds of
calculations that you can't do on it.) You need at least
one more function. One such function, for instance, is
the inverse of the function f(x)=x5+x. (There are
other functions that would also work, and some of them
are more interesting to mathematicians for various
reasons, but I like this one because it can be described
in fairly elementary terms.) That function, together
with the functions ![]() and addition, subtraction,
multiplication, and division is enough to give a formula
for the solution of the general 5th degree polynomial
equation in terms of the coefficients of the polynomial
- i.e., the degree 5 analogue of the quadratic formula.
But it's horribly complicated; I don't even want to think
about writing it down.
and addition, subtraction,
multiplication, and division is enough to give a formula
for the solution of the general 5th degree polynomial
equation in terms of the coefficients of the polynomial
- i.e., the degree 5 analogue of the quadratic formula.
But it's horribly complicated; I don't even want to think
about writing it down.