Browser adjustments: This web page uses
subscripts, superscripts, and unicode symbols. The latter may display
incorrectly on your computer if you
are using an old browser and/or an old operating system.
Note to teachers
(and anyone else who is interested):
Feel free to link to this page (around 500 people have done so), tell your students about this page, or
copy (with appropriate citation) parts or all of this
page. You can do those things without writing to me.
But if you have anything else to say about this page,
please write
to me with your questions, comments, or suggestions. I will
reply when I have time, though that might not be
immediately -- recently I've been swamped with other
work.
-- Eric
Schechter, version of 11 Nov 2009.
This web page describes the errors that I have seen most frequently in undergraduate mathematics, the likely causes of those errors, and their remedies. I am tired of seeing these same old errors over and over again. (I would rather see new, original errors!) I caution my undergraduate students about these errors at the beginning of each semester. Outline of this web page:
Some teachers are hostile to questions. That is an error made by teachers. Teachers, you will be more comfortable in your job if you try to do it well, and don't think of your students as the enemy. This means listening to your students and encouraging their questions. A teacher who only lectures, and does not encourage questions, might as well be replaced by a book or a movie. To teach effectively, you have to know when your students have understood something and when they haven't; the most efficient way to discover that is to listen to them and to watch their faces. Perhaps you identify with your brightest students, because they are most able to appreciate the beauty of the ideas you are teaching -- but the other students have greater need of your help, and they have a right to it.
A variant of teacher hostility is teacher arrogance. In its mildest form, this may simply mean a teacher who, despite being polite and pleasant, is unable to conceive of the idea that he/she could have made an error, even when that error is brought directly to his/her attention. Actually, most of the errors listed below can be made by teachers, not just by students. (However, most teachers are right far more often than their students, so students should exercise great caution when considering whether their teachers could be in error.)
If you're a student with a hostile teacher, then I'm afraid I don't know what advice to give you; transfer to a different section or drop the course altogether if that is feasible. The remarks on communication in the next few paragraphs are for students whose teachers are receptive to questions. For such students, a common error is that of not asking questions.
When your teacher says something that you don't understand, don't be shy about asking; that's why you're in class! If you've been listening but not understanding, then your question is not a "stupid question." Moreover, you probably aren't alone in your lack of understanding -- there are probably a dozen other students in your classroom who are confused about precisely the same point, and are even more shy and inarticulate than you. Think of yourself as their spokesperson; you'll be doing them all a favor if you ask your question. You'll also be doing your teacher a favor -- your teacher doesn't always know which points have been explained clearly enough and which points have not; your questions provide the feedback that your teacher needs.
If you think your teacher may have made a mistake on the chalkboard, you'd be doing the whole class a favor by asking about it. (To save face, just in case the error is your own, formulate it as a question rather than a statement. For instance, instead of saying "that 5 should be a 7", you can ask "should that 5 be a 7?")
And try to ask your question as soon as possible after it comes up. Don't wait until the very end of the example, or until the end of class. As a teacher, I hate it when class has ended and students are leaving the room and some student comes up to me and says "shouldn't that 5 have been a 7?" Then I say "Yes, you're right, but I wish you had asked about it out sooner. Now all your classmates have an error in the notes that they took in class, and they may have trouble deciphering their notes later."
Marc Mims sent me this anecdote about unasked questions:
In the early 1980s, I managed a computer retail store. Several of my employees were college students. One bright your man was having difficulty with his Freshman college algebra class. I tutored him and he did very well, but invariably, he would say, "the professor worked through this problem on the board, and it was nothing like this. I sure hope we got the correct answer."I accompanied him to class one morning and discovered the source of his frustration. The professor was from the music department, and didn't normally teach college algebra --- he had been pressed into duty when over enrollment forced the class to be split.
During the class, he picked a problem from the assignment to work out on the board. Very early in the problem, he made an error. I don't recall the specifics, but I'm sure it was one of the many typical algebra errors you list.
Because of the error, he eventually reached a point from which he could no longer proceed. Rather than admitting an error and going to work to find it, he paused staring at the board for several seconds, then turned to the class and said, "...and the rest, young people, should be obvious."
Unclear wording. The English language was not designed for mathematical clarity. Indeed, most of the English language was not really designed at all -- it simply grew. It is not always perfectly clear. Mathematicians must build their communication on top of English [or replace English with whatever is your native or local language], and so they must work to overcome the weaknesses of English. Communicating clearly is an art that takes great practice, and that can never be entirely perfected.
Lack of clarity often comes in the form of ambiguity -- i.e., when a communication has more than one possible interpretation. Miscommunication can occur in several ways; here are two of them:
One way that ambiguity can occur is when there are multiple conventions. A convention is an agreed-upon way of doing things. In some cases, one group of mathematicians has agreed upon one way of doing things, and another group of mathematicians has agreed upon another way, and the two groups are unaware of each other. The student who gets a teacher from one group and later gets another teacher from the other group is sure to end up confused. An example of this is given under "ambiguously written fractions," discussed later on this page.
Choosing precise wording is a fine art, which can be improved with practice but never perfected. Each topic within math (or within any field) has its own tricky phrases; familiarity with that topic leads to eventually mastering those phrases.
For instance, one student sent me this example
from combinatorics, a topic that requires somewhat awkward
English:
How many different words of five letters can be formed from seven
different consonants and four different vowels if no two consonants
and vowels can come together and no repetitions are allowed? How many can
be formed if each letter could be repeated any number of times?
There are a number of places where this problem is unclear. In
the first sentence, I'm not sure what "can come together" means,
but I would guess that the intended meaning is
How many different words of five letters can be formed from seven
different consonants and four different vowels if no two consonants
can occur consecutively and no two vowels can occur consecutively
and no repetitions are allowed?
The second sentence is a bit worse. The student misinterpreted
that sentence to mean
How many different words of five letters can be formed from seven
different consonants and four different vowels if
each letter could be repeated any number of times?
But usually, when a math
book asks two consecutive questions related in this fashion, the
second question is intended as a modification of the first
question. We are to retain all parts of the first question
that are compatible with the new conditions, and to discard
all parts of the first question that would be contradicted
by the new conditions. Thus,
the second sentence in our example should be interpreted
in this rather different fashion, which yields a different answer:
How many different words of five letters can be formed from seven
different consonants and four different vowels if no two consonants
can be consecutive, no two vowels can be consecutive, and
each letter could be repeated any number of times?
Bad handwriting is an error that the student makes in communicating with himself or herself. If you write badly, your teacher will have difficulty reading your work, and you may even have difficulty reading your own work after some time has passed!
Usually I do not deduct points for a sloppy handwriting style, provided that the student ends up with the right answer at the end -- but some students write so badly that they end up with the wrong answer because they have misread their own work. For instance,
By the way, write your plus sign (+) and lower-case letter Tee (t) so that they don't look identical! One easy way to do this is to put a little "tail" at the bottom of the t, just as it appears in this typeset document. (I assume that the fonts you're using on your browser aren't much different from my fonts.)
Not reading directions. Students often do not read the instructions on a test carefully, and so in some cases they give the right answer to the wrong problem.
Loss of invisible parentheses. This is not an erroneous belief;
rather, it is a sloppy technique of writing. During one of your computations,
if you think a pair of parentheses but neglect to write them (for
lack of time, or from sheer laziness), and then in the next step of your
computation you forget that you omitted a parenthesis from the previous
step, you may base your subsequent computations on the incorrectly written
expression. Here is a typical computation of this sort:
A partial loss of parentheses results in
unbalanced parentheses. For example, the expression
"3(5x4+2x+7" is meaningless, because there are
more left parentheses than right parentheses. Moreover, it
is ambiguous -- if we try to add a right parenthesis, we could
get either
Loss of parentheses is particularly common with minus signs and/or with integrals; for instance,
Terms lost inside an ellipsis. An ellipsis is three dots (...), used to denote
"continue the pattern". This notation can be used to write a long list. For instance,
The ellipsis notation conceals some terms in the sequence.
But can only be used if enough terms are left unconcealed to make the
pattern evident. For instance,
I have seen many errors in using ellipses when I've tried to teach induction proofs. For instance, suppose that we'd like to prove
[*n] 12 + 22 + 32 + ... + n2 = n(n+1)(2n+1)/6for all positive integers n. The procedure is this: Verify that the equation is true when n=1 (that's the "initial step); then assume that [*n] is true for some unspecified value of n and use that fact to prove that it's true for the next value of n -- i.e., to prove [*(n+1)] (that's the "transition step"). Here is a typical error in the transition step: Add
[i] 12 + 22 + 32 + ... + n2 + 2n+1 = (2n+1) + n(n+1)(2n+1)/6.But that says
[ii] 12 + 22 + 32 + ... + (n+1)2 = (2n+1) + n(n+1)(2n+1)/6.We've made a mistake already, in the left side of the equation. (Can you find it? I'll explain it in a moment.) Now make some algebra error while rearranging the right side of the equation, to obtain
[*(n+1)] 12 + 22 + 32 + ... + (n+1)2 = (n+1)(n+2)(2n+3)/6.And now it appears that we're done. But there was an algebra error on the right side:
The error on the left side was more subtle. It is based on the fact that too many terms were concealed in the ellipsis, and so the pattern was not revealed accurately. To see what is really going on, let's rewrite equations [i] and [ii], putting more terms in:
[i] 12 + 22 + 32 + ... + (n-2)2 + (n-1)2 + n2 + 2n+1 = (2n+1) + n(n+1)(2n+1)/6.And now you can see that the left side is missing its n2 term, so the left side of [ii] is not equal to the left side of [*(n+1)].[ii] 12 + 22 + 32 + ... + (n-2)2 + (n-1)2 + (n+1)2 = (2n+1) + n(n+1)(2n+1)/6.
Sign errors are surely the most common errors of all. I generally deduct only one point for these errors, not because they are unimportant, but because deducting more would involve swimming against a tide that is just too strong for me. The great number of sign errors suggests that students are careless and unconcerned -- that students think sign errors do not matter. But sign errors certainly do matter, a great deal. Your trains will not run, your rockets will not fly, your bridges will fall down, if they are constructed with calculations that have sign errors.
Sign errors are just the symptom; there can be several different underlying causes. One cause is the "loss of invisible parentheses," discussed in a later section of this web page. Another cause is the belief that a minus sign means a negative number. I think that most students who harbor this belief do so only on an unconscious level; they would give it up if it were brought to their attention. [My thanks to Jon Jacobsen for identifying this error.]
Is –x a negative number? That depends on what x is.
Another reason that
some students get confused on this point is that we read
Misunderstanding this point also causes some
students to have difficulty understanding the definition
of the absolute value function. Geometrically, we
think of |x| as the distance between x and 0. Thus
Those definitions of absolute value are all geometric or verbal or
algorithmic.
It is useful to also have a formula that defines
Many college students don't know how to add fractions.
They don't know how to add
Everything is additive. In advanced mathematics, a function or operation f is called additive if it satisfies f(x+y)=f(x)+f(y) for all numbers x and y. This is true for certain familiar operations -- for instance,
![[image:
sin(x+y) is NOT equal to sin x+sin y,
(x+y)^2 is NOT equal to x^2+y^2,
sqrt(x+y) is NOT equal to sqrt x+sqrt y,
1/(x+y) is NOT equal to (1/x)+(1/y).]](signxy.gif)
We do get equality holding for a few unusual and
coincidental choices of x and
y, but we have inequality for most choices of x
and y.
(For instance, all four of those lines are inequalities when
One explanation for the error with sines is that
some students, seeing the parentheses, feel that the sine
operator is a multiplication operator -- i.e., just as
The "everything is additive" error is actually the most common occurrence of a more general class of errors:
Everything is commutative. In higher mathematics, we say that two operations commute if we can perform them in either order and get the same result. We've already looked at some examples with addition; here are some examples with other operations. Contrary to some students' beliefs,
![[image:
log(sqrt x) is NOT equal to sqrt(log x),
sin(3x) is NOT equal to 3(sin x),]](logsqrtx.gif)
etc.
Another common error is to assume that multiplication commutes
with differentiation or integration. But actually, in general
However, to be completely honest about this, I must admit that there is one very special case where such a multiplication formula for integrals is correct. It is applicable only when the region of integration is a rectangle with sides parallel to the coordinate axes, and
u(x) is a function that depends only on x (not on y), andUnder those conditions,
v(y) is a function that depends only on y (not on x).
![[image: double integral, from a to b and from c to d, of
u(x)v(y)dydx, is equal to the product of these two
integrals: integral from a to b of u(x)dx and integral
from c to d of v(y)dy.]](recintgl.gif)
Undistributed cancellations. Here is an error that I have seen fairly often, but I don't have a very clear idea why students make it.
| (3x+7)(2x–9) + (x2+1) | (2x–9) + (x2+1) | ||||
| f(x) = |
| = | |||
| (3x+7)(x3+6) | (x3+6) |
In a sense, this is the reverse of the "loss of invisible parentheses" mentioned earlier; you might call this error "insertion of invisible parentheses." To see why, compare the preceding computation (which is wrong) with the following computation (which is correct).
| (3x+7) [ (2x–9) + (x2+1)] | (2x–9) + (x2+1) | ||||
| g(x) = | = | = | |||
| (3x+7) (x3+6) | (x3+6) |
Apparently some students think that f(x) and g(x) are the same thing -- or perhaps they simply don't bother to look carefully enough at the top line of f(x), to discover that not everything in the top line of f(x) has a factor of (3x+7). If you still don't see what's going on, here is a correct computation involving that first function f :
| x2+1 | ||||
| 2x–9 + | ||||
| (3x+7)(2x–9) + (x2+1) | 3x+7 | |||
| f(x) = | = | |||
| (3x+7)(x3+6) | x3+6 | |||
(x1+x2)y=(x1y)+(x2y) and x(y1+y2)=(xy1)+(xy2) .
(x1+x2)/y = (x1/y)+(x2/y) but in general x/(y1+y2) ≠ (x/y1)+(x/y2) .
| a+b |
| c+d |
Dimensional errors. Most of this web page is devoted to things that you should not do, but dimensional analysis is something that you should do. Dimensional analysis doesn't tell you the right answer, but it does enable you to instantly recognize the wrongness of some kinds of wrong answers. Just keep careful track of your dimensions, and then see whether your answer looks right. Here are some examples:
Here is a cute example of dimensional analysis (submitted by Benjamin Tilly).
Problem: Where has my money gone? My dollar seems to have turned into a penny:
$1 = 100¢ = (10¢)2 = ($0.10)2 = $0.01 = 1¢
Explanation: Of course, the problem is a disregard for dimensional units. Strictly speaking, if you square a dollar, you should get a square dollar. I don't know what a "square dollar" is, but I still know how to compute with it, and I know that a "square dollar" must be equal to 10,000 "square pennies", since one dollar is 100 pennies. Dimensional computations will not yield errors if we handle the dimensional units correctly. Here is a correct computation:
$21 = ($1)2 = (100¢)2 = 1002¢2 = 10,000¢2.It should now be evident what was wrong with the first calculation: 100¢ is not equal to (10¢)2. It's true that the 100 is equal to the 102, but the ¢ is not equal to ¢2. Likewise, later in the computation, $2 is not equal to $.
Idiosyncratic inverses. We need to be sympathetic about the student's difficulty in learning the language of mathematicians. That language is a bit more consistent than English, but it is not entirely consistent -- it too has its idiosyncrasies, which (like those of English) are largely due to historical accidents, and not really anyone's fault. Here is one such idiosyncrasy: The expressions sinn and tann get interpreted in different ways, depending on what n is.
sin2x = (sin x)2 and tan2x = (tan x)2;but
sin–1x = arcsin(x) and tan–1x = arctan(x).Some students get confused about this; some even end up setting
Confusion about the square root symbol. Every positive number b has two square roots. The expression √b actually means "the nonnegative square root of b," but unfortunately some students think that that expression means "either of the square roots of b" -- i.e., they think it represents two numbers. ... This error is made more common because of the unfortunate fact that we math teachers are merely human, and sometimes a little sloppy: When we write √b on the blackboard, what we say aloud might just be "the square root of b." But that's just laziness. If you ask us specifically about that, we'll tell you "Oh, I'm sorry, of course I meant the nonnegative square root of b; I thought that goes without saying." ... If you really do want to indicate both square roots of b, you use the plus-or-minus sign, as in this expression: ±√b.
Problems with order of operations. It is customary to
perform certain mathematical operations in certain orders,
and so we don't need quite so many parentheses. For
instance, everyone agrees that
Here is an example from
Ian Morrison:
What is
Ambiguously written fractions.
In certain common situations with fractions, there is a
lack of consensus about what order to perform
operations in. For instance,
does
For this confusion, teachers must share the blame. They certainly mean well -- most math teachers believe that they are following the conventional order of operations. They are not aware that several conventions are widely used, and no one of them is universally accepted. Students may learn one method from one teacher and then go on to another teacher who expects students to follow a different method. Both teacher and student may be unaware of the source of the problem.
Here are some of the most widely used interpretations:
Some students think that their electronic calculators can be relied upon for correct answers. But some calculators follow one convention, and other calculators follow another convention. In fact, some of the Texas Instruments calculators follow two conventions, according to whether multiplication is indicated by juxtaposition or a symbol:
Because there is no consensus of interpretation,
I recommend that
you do not write expressions like ![]() , 3/(5x),
, 3/(5x),
![]() .
.
In some cases, additional information is evident from the context --
if one is familiar with the context. For instance, an experienced
mathematician will recognize
Here is another common error in the writing of fractions:
If you write
the horizontal fraction bar too high, it can be misread. For instance,
![]() or
or
![]() are
acceptable expressions (with different meanings), but
are
acceptable expressions (with different meanings), but
![]() is
unacceptable -- it has no conventional meaning, and could be interpreted
ambiguously as either of the previous fractions.
I will not give full credit for ambiguous answers on any quiz or test.
In this type of error,
sloppy handwriting is the culprit. When you write an expression
such as
is
unacceptable -- it has no conventional meaning, and could be interpreted
ambiguously as either of the previous fractions.
I will not give full credit for ambiguous answers on any quiz or test.
In this type of error,
sloppy handwriting is the culprit. When you write an expression
such as ![]() ,
be sure to write carefully, so that the horizontal bar is aimed at the
middle of the x.
,
be sure to write carefully, so that the horizontal bar is aimed at the
middle of the x.
Here's one more example of interest.
When entered as
Stream-of-consciousness equalities and implications. (My thanks to H. G. Mushenheim for identifying this type of error and suggesting a name for it.) This is an error in the intermediate steps in students' computations. It doesn't often lead to an erroneous final result at the end of that computation, but it is tremendously irritating to the mathematician who must grade the student's paper. It may also lead to a loss of partial credit, if the student makes some other error in his or her computation and the grader is then unable to decipher the student's work because of this stream-of-consciousness error.
To put it simply: Some students (especially college freshmen)
use the equals sign (=) as a symbol
for the word "then" or the phrase "the next step is."
For instance, when asked to find the third derivative of
A slight
variant of this error consists of connecting several different
equations with equal signs, where the intermediate
equals signs are intended to convey "equivalent to" --- for example,
There is also a more "advanced" form of this error. Some more advanced students (e.g., college seniors) use the implication symbol (⇒) as a symbol for the phrase "the next step is." A string of statements of the form
Actually, there is a symbol for "the next step is." It looks like this:
![]() It is also called "leads to," and in the LaTeX formatting language
it is given by the code \leadsto. However, I haven't
seen it used very often.
It is also called "leads to," and in the LaTeX formatting language
it is given by the code \leadsto. However, I haven't
seen it used very often.
Going over your work. Unfortunately, most textbooks do not devote a lot of attention to checking your work, and some teachers also skip this topic. Perhaps the reason is that there is no well-organized body of theory on how to check your work. Unfortunately, some students end up with the impression that it is not necessary to check your work -- just write it up once, and hope that it's correct. But that's nonsense. All of us make mistakes sometimes. In any subject, if you want to do good work, you have to work carefully, and then you have to check your work. In English, this is called "proofreading"; in computer science, this is called "debugging."
Moreover, in mathematics, checking your work is an important part of the learning process. Sure, you'll learn what you did wrong when you get your homework paper back from the grader; but you'll learn the subject much better if you try very hard to make sure that your answers are right before you turn in your homework.
It's important to check your work, but "going over your work" is the worst way to do it. I have twisted some words here, in order to make a point. By "going over your work" I mean reading through the steps that you've just done, to see if they look right. The drawback of that method is you're quite likely to make the same mistake again when you read through your steps! This is particularly true of conceptual errors -- e.g., forgetting to check for extraneous roots (discussed later on this web page).
You would be much more likely to catch your error if, instead, you checked your work by some method that is different from your original computation. Indeed, with that approach, the only way your error can go undetected is if you make two different errors that somehow, just by a remarkable coincidence, manage to cancel each other out -- e.g., if you arrive at the same wrong answer by two different incorrect methods. That happens occasionally, but very seldom.
In many cases, your second method can be easier, because it can make use of the fact that you already have an answer. This type of checking is not 100% reliable, but it is very highly reliable, and it may take very little time and effort.
Here is a simple example. Suppose that we want to solve 3(x–2)+7x = 2(x+1) for x. Here is a correct solution:
Now, one easy way to check this work is to plug
Different kinds of problems require different kinds of checking. For a few kinds of problems, no other method of checking besides "going over your work" will suggest itself to you. But for most problems, some second method of checking will be evident if you think about it for a moment.
If you absolutely can't think of any other method, here is a last-resort technique: Put the paper away somewhere. Several hours later (if you can afford to wait that long), do the same problems over -- by the same method, if need be -- but on a new sheet of paper, without looking at the first sheet. Then compare the answers. There is still some chance of making the same error twice, but this method reduces that chance at least a little. Unfortunately, this technique doubles the amount of work you have to do, and so you may be reluctant to employ this technique. Well, that's up to you; it's your decision. But how badly do you want to master the material and get the higher grade? How much importance do you attach to the integrity of your work?
One method that many students use to check their homework is this: before turning in your paper, compare it with a classmate's paper; see if the two of you got the same answers. I'll admit that this does satisfy my criterion: If you got the same answer for a problem, then that answer is probably right. This approach has both advantages and disadvantages. One disadvantage is that it may violate your teacher's rules about homework being an individual effort; perhaps you should ask your teacher what his or her rules are. Another concern is: how much do you learn from the comparison of the two answers? If you discuss the problem with your classmate, you may learn something. With or without a classmate's involvement, if you think some more about the different solutions to the problem, you may learn something.
When you do find that your two answers differ, work very carefully to determine which one (if either) is correct. Don't hurry through this crucial last part of the process. You've already demonstrated your fallibility on this type of problem, so there is extra reason to doubt the accuracy of any further work on this problem; check your results several times.
Perhaps the error occurred through mere carelessness, because you weren't really interested in the work and you were in a hurry to finish it and put it aside. If so, don't compound that error. You now must pay for your neglect -- you now must put in even more time to master the material properly! The problem won't just go away or lose importance if you ignore it. Mathematics, more than any other subject, is vertically structured: each concept builds on many concepts that preceded it. Once you leave a topic unmastered, it will haunt you repeatedly throughout many of the topics that follow it, in all of the math courses that follow it.
Also, if discover that you've made an error, try to discover what the error was. It may be a type of error that you are making with some frequency. Once you identify it, you may be better able to watch out for it in the future.
Not noticing that some steps are irreversible. If you do the same thing to both sides of a true equation, you'll get another true equation. So if you have an equation that is satisfied by some unknown number x, and you do the same thing to both sides of the equation, then the new equation will still be satisfied by the same number x. Thus, the new equation will have all the solutions x that the old equation had -- but it might also have some new solutions.
Some operations are reversible -- i.e., we have the same set of solutions before and after the operation. For instance,
A commonly used method for solving equations is this: Construct a sequence
of equations, going from one equation to the next by doing the same
thing to both sides of an equation, choosing the operations to gradually
simplify the equation, until you get the equation down to something
obvious like
| if any of your steps are irreversible, then you must check for extraneous roots when you get to the end of the computation. |
That's because, at the end of your computational procedure, you'll have not only the solution(s) to the original problem, but possibly also some additional numbers that do not solve the original problem. How do you check for them? Just plug each of your answers into the original problem, to see whether it works. Many students, unfortuntely, omit that last step.
First example:
![[image: square root of (2x+12)]](sqrt2x12.gif) – 2 = x.
– 2 = x.![[image: square root of (2x+12)]](sqrt2x12.gif) = x + 2.
= x + 2.
Unfortunately, many students stop at this step; they
believe they're done; they write
![[image: square root of (2x+12)]](sqrt2x12.gif) – 2 =
(4+12)1/2 – 2 =
4 – 2 = x,
so we
have a correct solution. However,
– 2 =
(4+12)1/2 – 2 =
4 – 2 = x,
so we
have a correct solution. However,
![[image: square root of (2x+12)]](sqrt2x12.gif) – 2 =
(–8+12)1/2 – 2 =
2 – 2 ≠ x,
so we
have an incorrect solution.
– 2 =
(–8+12)1/2 – 2 =
2 – 2 ≠ x,
so we
have an incorrect solution.
Thus the correct answer is
![[image: (x^3-3)/x + (3x^2+x+7)/x = 1 + (4/x)]](belfrac1.gif) .
By adding and subtracting (reversible), we obtain
.
By adding and subtracting (reversible), we obtain
![[image: (x^3+3x^2)/x=0]](belfrac2.gif) .
By factoring (reversible), we obtain
.
By factoring (reversible), we obtain
![[image: x^2(x+3)/x=0]](belfrac3.gif) .
Cancel out an x (irreversible); we obtain
.
Cancel out an x (irreversible); we obtain Of course, even aside from the issue of extraneous roots, another reason to check your answers is to avoid arithmetic errors. This is a special case of "checking your work," mentioned elsewhere on this web page. We all make computational mistakes; we can catch most of our computational mistakes with a little extra effort.
The extraneous roots error was brought to my attention by Dr. Richard Beldin. Professor Beldin tells me that he gave a test heavily laced with extraneous roots problems, and warned the students that
Confusing a statement with its converse. The implication "A implies B" is not the same as the implication "B implies A." For instance,
if I went swimming at the beach today, then I got wet todayis a true statement. But
if I got wet today, then I went swimming at the beach todaydoesn't have to be true -- maybe I got wet by taking a shower or bath at home. The difference is easy to see in concrete examples like these, but it may be harder to see in the abstract setting of mathematics.
Some technical terminology might be helpful here.
The symbol
⇒ means "implies."
The two statements
"
I should emphasize the word "generally" in the
last paragraph. In a few cases the implications
"
p2+q2=r2 if and only if the triangle is a right triangle.The "if" part of that statement is the well-known Pythagorean Theorem; the "only if" part is its converse, which also happens to be true but is less well known.
Some students confuse a statement with its converse. This may stem partly from the fact that, in many nonmathematical situations, a statement is equivalent to its converse, and so in everyday "human" English we often use the word "if" interchangeably with the phrase "if and only if". For instance,
I'll go to the vending machine and buy a snack if I get hungrysounds reasonable. But most people would figure that if I do not get hungry, then I won't go buy a snack. So, evidently, what I really meant was
I'll go to the vending machine and buy a snack if and only if I get hungry.Most people would just say the shorter sentence, and mean the longer one; it's a sort of verbal shortcut. Generally you can figure out from the context just what the real meaning is, and usually you don't even think about it on a conscious level.
To make matters more confusing, mathematicians are humans too. In certain contexts, even mathematicians use "if" when they really mean "if and only if." You have to figure this out from the context, and that may be hard to do if you're new to the language of mathematics, and not a fluent speaker. Chiefly, mathematicians use the verbal shortcut when they're giving definitions, and then you have a hint: the word being defined usually is in italics or boldface. For instance, here is the definition of continuity of a real-valued function f:
f is continuous if for each real number p and each positive number ε there exists a positive number δ (which may depend on p and ε) such that, for each real number q, ifThe fourth word in this very long sentence is an "if" that really means "if and only if", but we know that because "continuous" is in boldface; this is the definition of the word "continuous".| p - q | < δ , then| f(p) - f(q) | < ε.
Converses also should not be confused with
contrapositives. Those two words sound similar
but they mean very different things.
The contrapositive of the implication
"
if I went swimming at the beach today, then I got wet todayhas exactly the same meaning as the more complicated sounding statement
if I didn't get wet today, then I didn't go swimming at the beach today.Sometimes we replace a statement with its contrapositive, because it may be easier to prove, even if it is more complicated to state. (Thanks to Valery Mishkin for bringing this class of errors to my attention.)
Working backward. This is an unreliable method of proof used,
unfortunately,
by many students. We start with the statement that we
want to prove, and gradually replace it with consequences,
until we arrive at a statement that is obviously true
(such as
Here is an example of a successful and correct use of "working backward": we are asked to prove that the cube root of 3 is greater than the square root of 2. We write these steps:
Working backward can be a good method for discovering proofs,
though it has to be used with caution, as discussed below.
But it is an unacceptable method for presenting proofs
after you have discovered them. Students must distinguish between
discovery (which can be haphazard, informal, illogical) and
presentation (which must be rigorous).
The reasoning used in
working backward is a reversal of the reasoning needed for
presentation of the proof -- but that means replacing
each implication
"
In some cases, the implication is reversible -- i.e., some reversible operation (like multiplying both sides of an equation by 2, or raising both sides of an inequality to the sixth power when both sides were already positive) transforms statement A into statement B. Perhaps the students have gotten into the habit of expecting all implications to be reversible, because early in their education they were exposed to many reversible transformations -- adding three, multiplying by a half, etc. But in fact, most implications of mathematical statements are not reversible, and so "working backward" is almost never acceptable as a method of presenting a proof.
Working backward can be used for discovering a proof (and, in fact, sometimes it is the only discovery method available), but it must be used with appropriate caution. At each step in the discovery process, you start from some statement A, and you create a related statement B; it may be the case that the implication A implies B is obvious. But you have to think about whether B implies A. If you can find a convincing demonstration that B implies A, then you can proceed. If you can't find a demonstration of B implies A, then you might as well discard statement B, because it is of no use at all to you; look for some other statement to use instead.
Beginners often make mistakes when they use "working backward,"
because they don't notice that some step is irreversible.
For instance, the statement
![[image: square root of (x^2-1)]](sqrtmin1.gif)
![[image: square root of (x^2-1)]](sqrtmin1.gif) .
.![[image: square root of (x^2-1)]](sqrtmin1.gif) means
the nonnegative square root of
means
the nonnegative square root of
![[image: square root of (x^2-1)]](sqrtmin1.gif)
Well then, if reasoning backward is not acceptable as a presentation of a proof, what is acceptable? A direct proof is acceptable. A theorem has certain hypotheses (assumptions) and certain conclusions. In a direct proof, you start with the hypotheses, and you generate consequences -- i.e., you start making sentences, where each sentence is either a hypothesis of the theorem, an axiom (if you're using an abstract theory), or a result deduced from some earlier theorem using sentences you've already generated in the proof. They must be in order -- i.e., if one sentence A is used to deduce another sentence B, then sentence A should appear before sentence B. The goal is to eventually generate, among the consequences, the conclusion of the desired theoreom.
Some variants on this are possible, but only if the explanatory language is used very carefully; such variants are not recommended for beginners. The variants involve phrases like "it suffices to show that...". These phrases are like foreshadowing in a story, or like direction signs on a highway. They intentionally appear out of chronological order, to make the intended route more understandable. But in some sense they are not really part of the official proof; they are just commentaries on the side, to make the official proof easier to understand. When you pass a sign that says "100 miles to Nashville," you're not actually in Nashville yet.
Perhaps the biggest failure in the proofs of beginners is a severe lack of words. A beginner will write down an equation that should be accompanied by either the phrase "we have now shown" or the phrase "we intend to show", to clarify just where we are in the proof. But the beginner writes neither phrase, and the reader is expected to guess which it is. This is like a novel in which there are many flashbacks and also much foreshadowing, but all the verbs are in present tense; the reader must try to figure out a logical order in which the events actually occur.
One easy method that I have begun recommending to students is this: Put a questionmark over any relationship (equals sign, greater than sign, etc.) that represents an assertion that you want to prove, but have not yet proved. An equals-sign without a questionmark will then be understood to represent an equation that you have already proved. Later you can put a checkmark next to the equations whose doubt has been removed. This method may help the student writing the work, but unfortunately it does not greatly help the teacher or grader who is reading the work -- the order of steps is still obscured.
Another common style of proof is the indirect proof,
also known as proof by contradiction.
In this proof, we start with the hypotheses of the desired
theorem; but we may also add, as additional hypothesis,
the statement that "the desired theorem's conclusion is
false." In other words, we really want to prove
Difficulties with quantifiers. Quantifiers are the phrases "there exists" and "for every." Many students -- even beginning graduate students in mathematics! -- have little or no understanding of the use of quantifiers. For instance, which of these statements is true and which is false, using the standard real number system?
For each positive number a there exists a positive number b such that b is less than a.Difficulty with quantifiers may be common, but I'm not sure what causes the difficulty. Perhaps it is just that mathematical sentences are grammatically more complicated than nonmathematical ones. For instance, a real-valued function f defined on the real line is continuous ifThere exists a positive number b such that for each positive number a we have b less than a.
for each point p and for each number epsilon greater than zero, there exists a number delta greater than zero such that, for each point q, if the distance from p to q is less than delta, then the distance from f(p) to f(q) is less than epsilon.This sentence involves several nested clauses, based on several quantifiers:
I think that many students would benefit from thinking of quantifiers as indicators of a competition between two adversaries, as in a court of law. For instance, when I assert that the function f is continuous, I am asserting that
no matter what point p and what positive number epsilon you specify, I can then specify a corresponding positive number delta, such that, no matter what point q you then specify, if you demonstrate that your q has distance from your p less than my delta, then I can demonstrate that the resulting f(p) and f(q) are separated by a distance less than your epsilon.Of course, it must be understood that the two adversaries in mathematics are emotionally and morally neutral. In a court of law (at least, as depicted on television), it is often the case that one side is the "good guys" and the other side is the "bad guys," but in principle the law is supposed to be a neutral way of seeking the truth; mathematical reasoning is too.
Some students may have an easier time avoiding errors with quantifiers if they actually use symbols instead of words. This may make the differences in the quantifiers more visually prominent. The symbols to use are
| universal quantifier | "for all" (or "for each") | |
| existential quantifier | "there exists" (or "there exists at least one") |
(Now you can see the four nested quantifiers very clearly; this may explain why the definition is so complicated -- and perhaps it will help to clarify what the definition means.p) (
ε>0) (
δ>0) (
q) (if |p–q|<δ, then |f(p)–f(q)|<ε).
Some readers have requested that I add a few words about negations of quantifiers.
The basic rules are these:
![]() =
=![]() ~
~![]() =
=![]() ~
~![]() =
=![]() ~
~
Saying "not every peanut in this jar is stale" is the same thing as saying "at least one peanut in this jar is not stale."An example of
Saying "there does not exist a stale peanut in this jar" is the same thing as saying "every peanut in this jar is non-stale."Here is a more complicated example: Following are a few different ways to say that "f is not continuous". Start with the formula that I gave above, but with a "not" in front of it. Gradually move the "not" to the right, switching each quantifier that it passes. So all these statements are equivalent:
Erroneous method justified by one or two instances of correct results. Sometimes an erroneous method can lead (just by coincidence) to a correct result. But that does not justify the method.
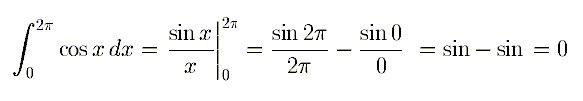
Unquestioning faith in calculators. Many students believe that their calculators are always right. But that is not true. All calculators have limitations, and will give incorrect answers under some circumstances (as will math teachers and math books).
Probably the most common error with calculators is simply forgetting to switch between degrees and radians (or not understanding the need to switch). Degrees are often used in engineering and science classes, but radians are almost always used in calculus and higher math classes. That's because most of the formulas involving trigonometric functions come out much simpler with radians than with degrees -- the formulas for the derivatives, for the power series expansions, etc.
Here is another widely occurring calculator error.
Some graphing calculators, if asked to display a graph of
Why is that? Well, first you need to understand that for
some constants k, the correct graph of
Dave Rusin has put together some notes on the wide variety of errors one can make by not understanding one's calculator. By the way, I'll take this opportunity to mention that Dave Rusin has put together a super website, Mathematical Atlas: A gateway to Mathematics, which offers definitions, introductions, and links to all sorts of topics in math.
A formula or notation may work properly in one context, but some students try to apply it in a wider context, where it may not work properly at all. Robin Chapman also calls this type of error "crass formalism." Here is one example that he has mentioned:
Every positive number has two square roots: one
positive, the other negative. The notation √b
generally
is only used when b is a nonnegative real number; it means
"the nonnegative square root of b," and not just "the
square root of b."
The notation √b probably should not
be used at all in the context of complex numbers.
Every nonzero complex number b has
two square roots, but in general there is no natural
way to say which one should be associated with the
expression
√b.
The formula
![]() is correct when a and b are
positive real numbers, but it leads to errors when
generalized indiscriminately to other kinds of
numbers. Beginners in the use
of complex numbers are prone to errors such as
is correct when a and b are
positive real numbers, but it leads to errors when
generalized indiscriminately to other kinds of
numbers. Beginners in the use
of complex numbers are prone to errors such as
![]() .
In fact, the great
mathematician Leonhard Euler published a computation
similar to this in a book in 1770, when the theory of
complex numbers was still young.
.
In fact, the great
mathematician Leonhard Euler published a computation
similar to this in a book in 1770, when the theory of
complex numbers was still young.
Here is another example, from my own teaching experience:
What is the derivative of xx? If you ask this during
the first week of calculus, a correct answer is "we haven't covered
that yet." But many students will very confidently tell you that the
answer is ![]() (xx) = xx (1 + ln x).
(xx) = xx (1 + ln x).
The difficulty is that, in high school or shortly after they arrive
at college, the students have learned that
That formula is actually WRONG, but in a very subtle way. The correct formula is
The equation is unchanged, but it's now accompanied by some
words telling us when the equation is applicable.
I've thrown in the parenthetical "for all x where the right side is
defined," in order to avoid discussing the complications that
arise when
To most teachers, that additional phrase doesn't seem important, because in the teacher's mind "x" usually means a variable and "k" usually means a constant. The letters x and k are used in different ways here, a little like the difference between bound and free variables in logic: Fix any constant k; then the equation states a relationship between two functions of the variable x. So the language suggests to us that x is probably not supposed to equal k.
But the math teacher is already fluent in this language, whereas mathematics is a foreign language to most students. To most students, the distinction between the two boxed formulas is one which doesn't seem important at first, because the only examples shown to the student at first are those in which k actually is a constant. Why bother to mention that k must be a constant, when there are no other conceivable meanings for k? So the student memorizes the first (incorrect) formula, rather than the second (correct) formula.
Every mathematical formula should be accompanied by a few words of English (or your natural language, whatever it is). The words in English tell when the formula can or can't be applied. But frequently we neglect the words, because they seem to be clear from the context. When the context changes, the words that we've omitted may become crucial.
Students have difficulty with this. Here is an experiment that I have
tried a few times: At the beginning of the semester, I tell the students
that the correct answer to
![]() (xx)
(xx)
I have a couple of theories about why this happens: (i) For most students, mathematics is a foreign language, and the student focuses his or her attention on the part which seems most foreign -- i.e., the formulas. The words have the appearance of something familiar ("oh, that's just English, and I already know English"), and so the student doesn't pay a lot of attention to the words. (ii) Undergraduate students tend to focus on mechanical computations; they are not yet mathematically mature enough to be able to think easily about theoretical and abstract ideas.
A sort of footnote: Here is a common error among readers of
this web page. Several people have written to me to
ask, shouldn't that formula say
"if k is any constant except 0", or
"if k is any constant except
Jumping to conclusions about infinity. Some problems involving infinity can be solved using "the elementary arithmetic of infinity". Some students jump to the conclusion that all problems involving infinity can be solved by this sort of "elementary arithmetic," and so they guess all sorts of incorrect answers (mainly 0 or infinity) to such problems.
Here is an example of the "elementary arithmetic": If we use the
equation cautiously, we can say (informally) that
![]()
Thus, the problem
![[image: as x goes to infinity, we have
these limits: x^3-x goes to infinity;
(x^2+(1/x))-x^2 goes to 0;
the square root of (x^2+x) minus x
goes to 1/2.]](infty4.gif)
In a similar fashion, ![]() do not have quick and easy answers; they too require more specialized and
sophisticated analyses.
do not have quick and easy answers; they too require more specialized and
sophisticated analyses.
Here is a common error mentioned by
Stuart Price:
Some students
seem to think that
That reminds me of a related
question that seems to bother many students:
What is
The reason that a question arises at all
is because
Nevertheless, many (most?) mathematicians will define 00 = 1, just for convenience, because that makes the most formulas work (and then they will note exceptions for formulas that require a different definition).
For instance, if we're working with polynomials or power series,
Problems with series.
Sean Raleigh reports that the most common series error he has seen is
this: If
Loss or misuse of constants of integration. The
indefinite integral
of a function involves an "arbitrary constant", and this causes
confusion
for many students, because the notation doesn't convey the
concept very well.
An expression such as
3x2+5x+7, 3x2+5x+19, 3x2+5x–3.19, etc.plus more functions of the same sort. One of the difficulties, also, is that the same letter "C" is customarily used for all such arbitrary constants; but one computation may involve several different arbitrary constants. It would be more accurate to put subscripts on the C's, to differentiate one of them from another -- i.e., write
Here is an example. The formula for Integration By Parts, in
its briefest form, is
| ∫u(x)v'(x)dx = u(x)v(x) - ∫u'(x)v(x)dx. |
Now, that formula is correct, but it can easily be mishandled and
can lead to errors. Here is
one particularly amusing error:
Plug
| ∫(1/x)(1)dx = (1/x)(x) - ∫(-1/x2)(x)dx |
which simplifies to
Now, regardless of what you think is
the value of
That is a true equation, if we choose the constants
Some students manage to make this kind of error even with
definite integrals.
They start from the formula
Some students may understand this better if we do the whole thing with definite integrals, right from the start. Let's use the formula
| ∫ab u(x)v′(x)dx = u(b)v(b) – u(a)v(a) – ∫ab u′(x)v(x)dx. |
Note that this formula has one more term than my previous boxed
formula -- when we convert
which (assuming 0 is not in the interval
which is true -- i.e., there is no contradiction here.
Some students may be puzzled by the differences between the two versions of the Integration by Parts formula (in boxes, in the last few paragraphs). I will describe in a little more detail how you get from the definite integral formula (in the last box) to the indefinite integral formula (in the first box in this section). Think of a as a constant and b as a variable, and you'll get something like this:
Note that the
Handling constants of integration gets even more complicated in the first course on differential equations, and there are even more kinds of errors possible. I won't try to list all of them here, but here is the simplest and most common error that I've seen: In calculus, some students get the idea that you can just omit the "+C" in your intermediate computations, and then tack it on at the end of your answer, if you know which kinds of problems require an arbitrary constant. That will usually work in calculus, but it doesn't work in differential equations, because in differential equations the "C" can show up anywhere -- not necessarily as a "+C" at the end of the answer.
Here's a simple example: Let's solve the differential equation xy′+7=y (where y′ means dy/dx). One way to solve it is by the following steps:
Loss of differentials. This shows up both in differentiation and in integration. The "loss of differentials" is much like the "loss of invisible parentheses" discussed earlier in this document; it is a type of sloppy writing in intermediate steps which leads to actual errors in the final answer.
When students first begin to learn to differentiate, they are always differentiating with respect to the same variable, and so they see no reason to mention that variable. Thus, in differentiating the function y = f(x) = 7x3+5x, they may correctly write
The difficulty, of course, shows up when we arrive at the Chain Rule. Suddenly, the question is no longer "What is the derivative of y", but rather, "What is the derivative of y with respect to x? with respect to u? How are those two derivatives related?" The student who does not make a habit of distinguishing between dy/dx and dy/du in writing may also have difficulty distinguishing between them conceptually, and thus will have difficulty understanding the Chain Rule.
This also leads to difficulties with the "u-substitutions" rule, which is just the Chain Rule turned into a rule about integrals. For instance:
![[image: large table containing
several integral problems, common
wrong answers, and correct answers]](diffls2.gif)
For the first three problems, the student
is attempting to use the formula
For the last problem in the table above, the student is
attempting to use the formula
Another correct way to write the rule about logarithms is
![]() .
Since this expresses everything in terms of the variable x, it may
make errors less likely. Admittedly, it is a complicated looking formula,
but it is preferable to a wrong formula. The first, third, and fourth problems
in the preceding table all require more complicated methods; just using
logarithms won't solve the problems for you. The problem of integrating
.
Since this expresses everything in terms of the variable x, it may
make errors less likely. Admittedly, it is a complicated looking formula,
but it is preferable to a wrong formula. The first, third, and fourth problems
in the preceding table all require more complicated methods; just using
logarithms won't solve the problems for you. The problem of integrating
We should prohibit students from writing an integral sign without a
matching differential. Just as any "(" must be matched with a
")", so too any integral sign must be matched with a "dx"
or "du" or "dt" or whatever. The expression
![]() is
unbalanced, and should be prohibited. If we're considering a substitution
of u = 1+x2, then
is
unbalanced, and should be prohibited. If we're considering a substitution
of u = 1+x2, then
By the way, some students get confused about whether
These loss-of-differentials errors in differentiation and in integration can be caught easily by a bit of "dimensional analysis" (discussed earlier). To do that, it is useful to think in terms of "infinitesimals" -- i.e., numbers that are "infinitely small" but still not zero. Newton and Leibniz had infinitesimals in mind when they invented calculus 300 years ago, but they didn't know how to explain infinitesimals rigorously. Infinitesimals became unfashionable a century or two later, when rigorous epsilon-delta proofs were invented. If we use the real number system that most mathematicians use nowadays, there are no infinitesimals except 0. But in 1960 a logician named Abraham Robinson invented another kind of real number system that includes nonzero infinitesimals; he found a way to back up the Newton-Leibniz intuition with rigorous proofs.
With the Newton-Leibniz-Robinson viewpoint, think of dx and dy as infinitesimals. Now, dy/dx is a quotient of two infinitely small numbers, so it could be a medium-sized number. Thus an equation such as dy/dx = 6x2 could make sense. An equation such as dy = 6x2 cannot possibly be correct -- the left side is infinitely small, and the right side is medium-sized.
The summation sign ∑ means add together finitely or countably many things -- for instance,
![[image:
sum from j=1 to 5 of j-squared is 55;
sum from j=1 to infinity of 2 to the
power minus j is 1]](sums.gif)
but ∑ generally is not used for adding uncountably many things.
(Occasionally it is so used: The sum of an arbitrary collection of nonnegative real numbers is the sup of the sums of finitely many members of that collection. But all the interesting action is happening on a countable set. It can be proved that if more than countably many of those numbers being added are nonzero, the sum must be infinity. Also, there may be other, more esoteric uses for the symbol ∑. But this web page is intended for undergraduates.)
However, in some sense we add together uncountably
many things when we use an integral. An
equation such as
A related difficulty is in trying to understand what "differentials" are.
Most recent calculus books have a few pages on this topic, shortly before
or after the Chain Rule. I am very sorry that the authors of calculus
books have chosen to cover this topic at this point in the book. I think
they are making a big mistake in doing so. When I teach calculus, I skip
that section, with the intention of covering it in a later
semester. Here is why:
When y=f(x), then dy=f′(x)dx is really a function of two variables-- it is
a function of both x and dx. But in many calculus textbooks,
that fact is not confronted directly; it is
swept under the rug and hidden. Several hundred pages later in most calculus
textbooks, we are introduced to functions of two variables, and given a decent
notation for them -- e.g., we may have z = h(u,v). At this point the student
may begin to understand functions of two variables, and we have partial derivatives
etc. But before this point, we are not given any good notations for a function
of two variables. Our beginning math students have difficulty enough with
abstractions even when they are provided with decent notation; how can we
expect them to think abstractly without the notation? Thus, when
I teach calculus, I describe "dx" and "dy" as "pieces of the notation
 This web page was selected as the "cool math web page of the week",
for the week of May 22, 2002, by
KaBoL.
This web page was selected as the "cool math web page of the week",
for the week of May 22, 2002, by
KaBoL.