Solutions to Class 17
1. Consider the set V of all 2-vectors and define two operations:
If x = (a,b) and y = (c,d), then the sum is (a+c+1,b+d) and the scalar multiplication k(a,b) = (ka,kb).
V is not a vector space. This rule for the sum of two vectors does not satisfy the 6th property of a vector space. This property states that there is a zero n-vector such that
0 + A = A + 0 = A for every A.
In our algebraic system, the zero-vector must be (-1,0).
A + 0 = (a,b) + (-1,0) = (a - 1 + 1, b + 0) = (a, b).
However, this definition for the zero vector will not satisfy the 7th property.
0*A = 0 (the first 0 is the scalar 0 and the second is the zero-vector).
In our system, 0*x = (0*a,0*b) = (0,0), which is not equal to the zero-vector (-1,0). The 7th property does not work.
So, since one of the properties for a vector space does not hold in our algebraic system, V, it is not a vector space.
2. Find a function f(x) from C[0,1] which is a scalar multiple of x2 and whose norm is 1.
The definition for the norm of a function f(x) is
(∫01 f(x)2 dx ) 1/2
So, we want to find the scalar multiple, k, such that the square root of k2x4 integrated from 0 to 1 equals 1.
> sqrt(int(k2*x4,x=0..1))=1;
1/5 51/2 k = 1
When solving this, Maple did not take into account the lost negative sign when you square a number. Hence k = +/- square root of 5. So,
f(x) = +/- (5)1/2 * x2.
Homework Solution for Class 17 proof problem.
1. Consider the set R2 of all 2-vectors. Define a dot product in R2 in the
following way:
(a,b)(c,d)=ac+bd+(1/2)ad+(1/2)bc
Prove that this dot product satisfies the properties of dot products in Euclidean
vector spaces and thus R2 with this dot product is a Euclidean vector space.
The dot product of
n-vectors satisfies the following properties:
- <A,B>=<B,A> ;
- <(A+B),C>=<A,C>+<B,C> ;
- <(kA),B>=<A,(kB)>=k*<A,B> ;
- <A,A> is greater than or equal to 0. <A,A> is 0 if and only if A=0.
Proof of property one:
Let A = (a,b) and B = (c,d), we will work out the dot products A*B and B*A.
<A,B> = <(a,b),(c,d)> = ac + bd + (1/2)ad + (1/2)bc
<B,A> = <(c,d),(a,b)> = ca + db + (1/2)cb + (1/2)da
and since multiplication of scalars is commutative, and since the addition of scalars
is associative, the dot product <B,A> can be rewritten as
<B,A> = ac + bd + (1/2)ad + (1/2)bc,
which is the same as we got for A*B. Thus,A*B = B*A.
Proof of property two:
Let A = (a,b), B = (c,d), and C = (e,f).
We will work out both <(A+B),C> and <A,C>+<B,C>, remembering both the definitions of
vector addition and vector multiplication by a scalar.
<(A+B),C> = <((a,b)+(c,d)),(e,f)>
= <(a+c,b+d),(e,f)>
= (a+c)e + (b+d)f + (1/2)(a+c)f + (1/2)(b+d)e
= ae + ce + bf + df + (1/2)af + (1/2)cf + (1/2)be + (1/2)de
<A,C>+<B,C> = <(a,b),(e,f)> + <(c,d),(e,f)>
= ae + bf + (1/2)af + (1/2)be + ce + df + (1/2)cf + (1/2)de
And since scalar addition is associative, this can be rewritten as
<A,C>+<B,C> = ae + ce + bf + df + (1/2)af + (1/2)cf + (1/2)be + (1/2)de,
which is exactly what we got from <(A+B),C>.
Thus, <(A+B),C> = <A,C>+<B,C>.
Proof of property three:
Let A = (a,b), B = (c,d), and k=k.
We will now work out <(kA),B>, <A,(kB)>, k*<A,B>, remembering both the
definitions of vector addition and vector multiplication by a scalar.
<(kA),B> = <(k(a,b)),(c,d)>
= <(ka,kb),(c,d)>
= kac + kbd + (1/2)kad + (1/2)kbc
<A,(kB)> = <(a,b),(k(c,d))>
= akc + bkd + (1/2)akd + (1/2)bkc
and since scalar multiplication is associative,
<A,(kB)> = kac + kbd + (1/2)kad + (1/2)kbc
k*<A,B> = <k((a,b),(c,d))>
= k(ac + bd + (1/2)ad + (1/2)bc)
and from the distributive property of multiplication with respect to addition,
this equals:
k*<A,B> = kad + kbd + (1/2)kad + (1/2)kbc
We thus get the same answer for all three, we get that
<(kA),B>=<A,(kB)>=k*<A,B>.
Proof of property four:
Let A = (a,b), using the new definition of the dot product, we will compute A*
A.
<A,A> = <(a,b),(a,b)>
= aa + bb + (1/2)ab + (1/2)ba
Using our algebraic properties from high school, this can be rewritten as:
<A,A> = a2 + ab + b2
If a=0 then <A,A>=b2 which is non-negative. If a is not 0
then <A,A> can be represented as a2(x2+x+1) where x=b/a.
The polynomial x2+x+1 is always positive since its first
coefficient is greater than 0 and the discriminant is less
than zero. Since a2>0, we get that in this case also A*A>0.
Now we need to prove that <A,A>=0 if and only if A=0. If A=(0,0) then
<A,A>=02+0*0+02=0. Suppose that A=(a,b) and
<A,A>=0, that is a2+ab+b2=0. If a is not 0 then we can represent <A,A> as above:
<A,A>=a2(x2+x+1)
which cannot be zero. Similarly if b is not zero then <A,A>=b2(y2+y+1)
where y=b/a and again <A,A> is not zero. Thus if <A,A>=0 then
the only possibility is that a=b=0, i.e. A=0.
2. Let V be a Euclidean vector space. A parallelogram is a quadruple of
vectors
of the form (A,B,A,B). Define the diagonals of a parallelogram and prove that
the sum of squares of the lengths of diagonals is equal to the sum of squares of
the lengths of
the sides of the parallelogram.
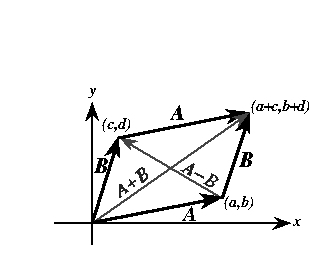
Let A=(a,b) and B=(c,d). The long diagonal of a parallelogram (A,B,A,B) equals
A+B, and the short diagonal of this paralelogram equals A-B.
Thus, the sum
of the squares of the diagonals (D) equals:
D = (A+B)2 + (A-B)2
= A2 + AB + B2 + A2 - AB + B2,
and since AB - AB = 0,
D = 2*A2 + 2*B2
We will now calculate the sum of the squares of the sides of the parallelogram (S).
S = A2 + B2 + A2 + B2
= 2*A2 + 2*B2
Thus, S = D, and the sum of squares of the lengths of diagonals is equal to the
sum of squares of the lengths of the sides of the parallelogram. The proof is
complete.
3. How would you define the sphere of radius r with center A in an arbitrary vector
space? Find all constant functions which belong to the sphere of radius 1 with
the center x2 in C[0,1].

By definition, a sphere is the set of points equidistant from a given center point. Therefore, we can define a sphere of radius r and center A in any vector space as the set of all vectors which are exactly a distance r from A. That is,
the sphere is the set of all vectors V such that d(A,V)=r if d(A,V) is the
distance between A and V. Computationally, we write ||A-V||=r.
So, for all constant functions f(x)=c in C[0,1], to find which ones are
members of the sphere with radius 1 and center x2, we merely need c to
satisfy ||c-x2|| = 1. To compute the left side of the equation, we use the
definition of the norm and the definition of the
dot product in C[0,1]:
||c-x2|| = (integral from 0 to 1 of (c-x2)*(c-x2) dx)1/2 = 1
By squaring both sides we achieve:
integral from 0 to 1 of (c - x2)*(c-x2) dx = 1
This is pretty easy to solve; just do an integral and solve a quadratic
equation in c.
> a:=(c - x2)*(c - x2);
a := (c - x2)2
> b:=int(a,x=0..1);
b := 1/5 + c2 - 2/3 c
This is equal to 1. Subtracting 1 from both sides and using the quadratic
equation we conclude that the values of c are:
> b1:=b-1;
b1 := - 4/5 + c2 - 2/3 c
> b2:= b1=0;
b2 := - 4/5 + c2 - 2/3 c = 0
> solve(b2);
1/3 + (1/15)411/2 51/2 , 1/3 - (1/15) 411/2 51/2
Return to Assignments


